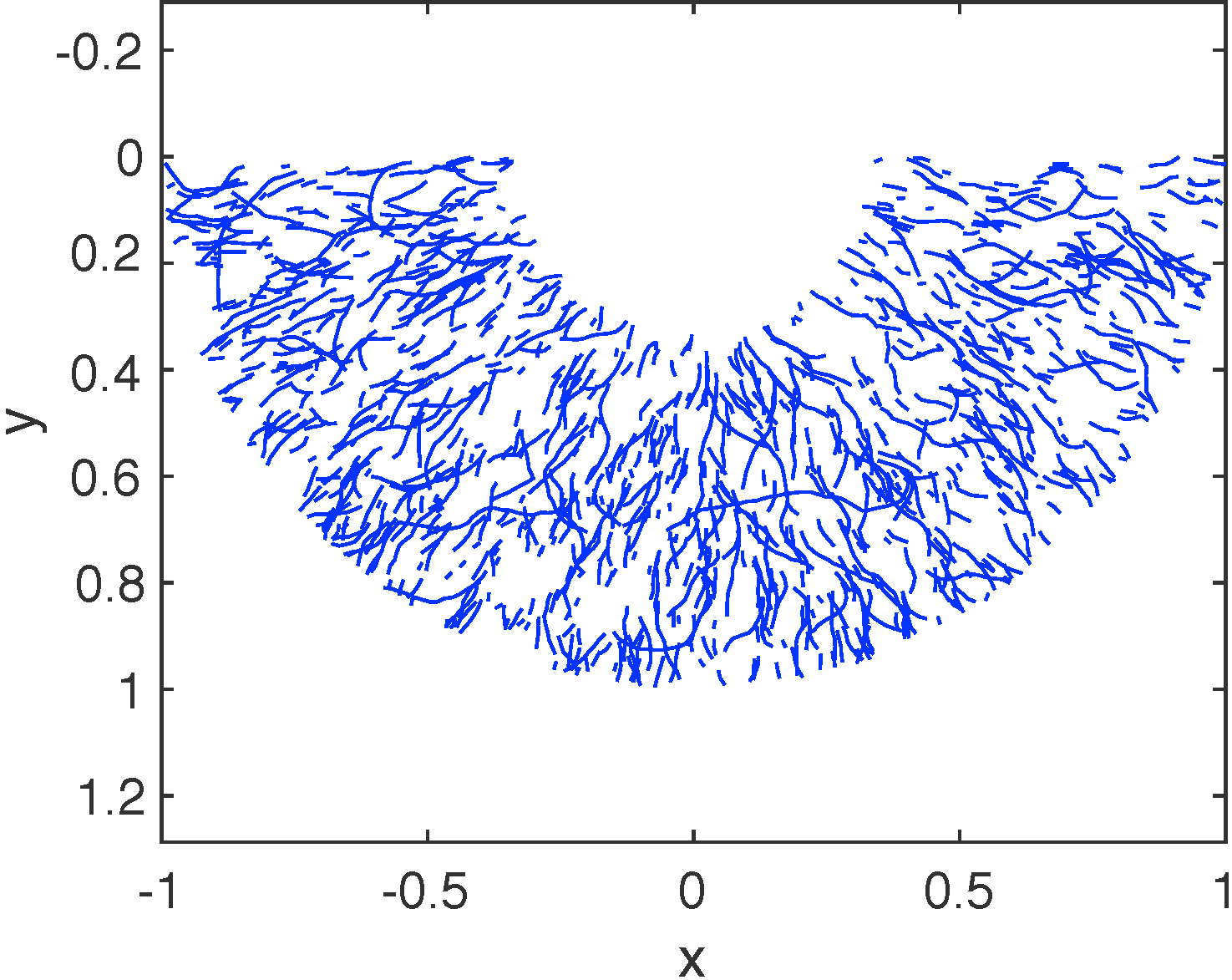
In my thesis research, I am interested in understanding spatial differentiation in early developing organisms. In particular, I model the accumulation of messenger RNA to different spatial areas (mRNA localization) in frog egg cells using systems of advection-reaction-dffusion PDEs, and estimate transport parameters using fluorescence recovery after photobleaching (FRAP) data. We use dynamical systems and stochastic methods to analyze the transport models and provide predictions for mRNA localization. Currently we are focused on analysis of nonlinear PDE models of mRNA transport and numerical simulations of the dynamics with transport restricted to the model microtubule structures.

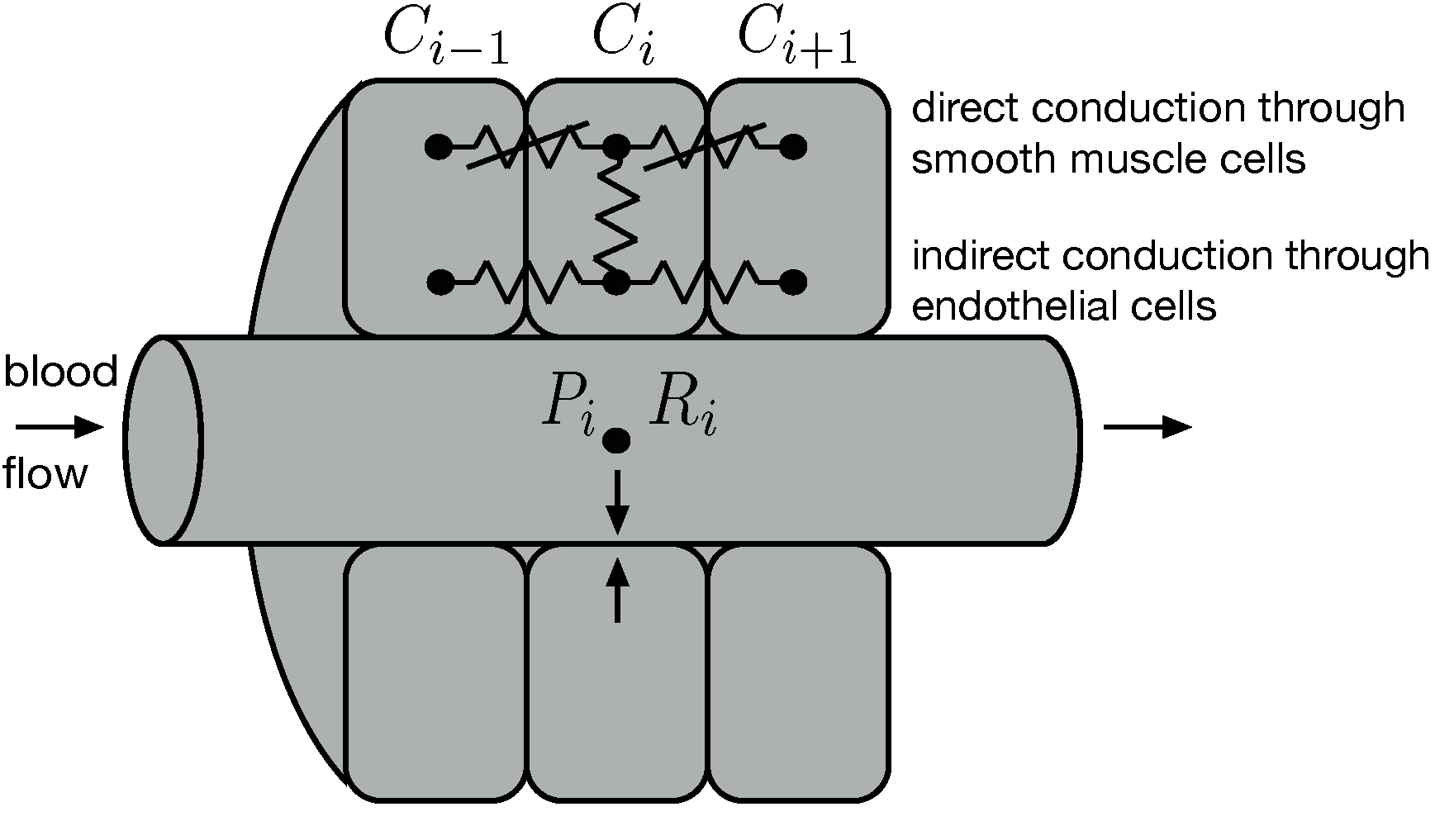
In this project, we are interested in understanding the mechanisms that lead to stable kidney filtration rate through a decrease (increase) in the diameter of kidney vessels when subjected to increased (decreased) blood pressure. We use a comprehensive model of differential equations to model the response of a multi-cell kidney vessel to different inflow blood pressures and perturbations. One of the key autoregulatory mechanisms we study is the myogenic response, which is used by the kidney to control blood flow. This research started during the Research Collaboration Workshop for Women in Mathematical Biology at NIMBioS.

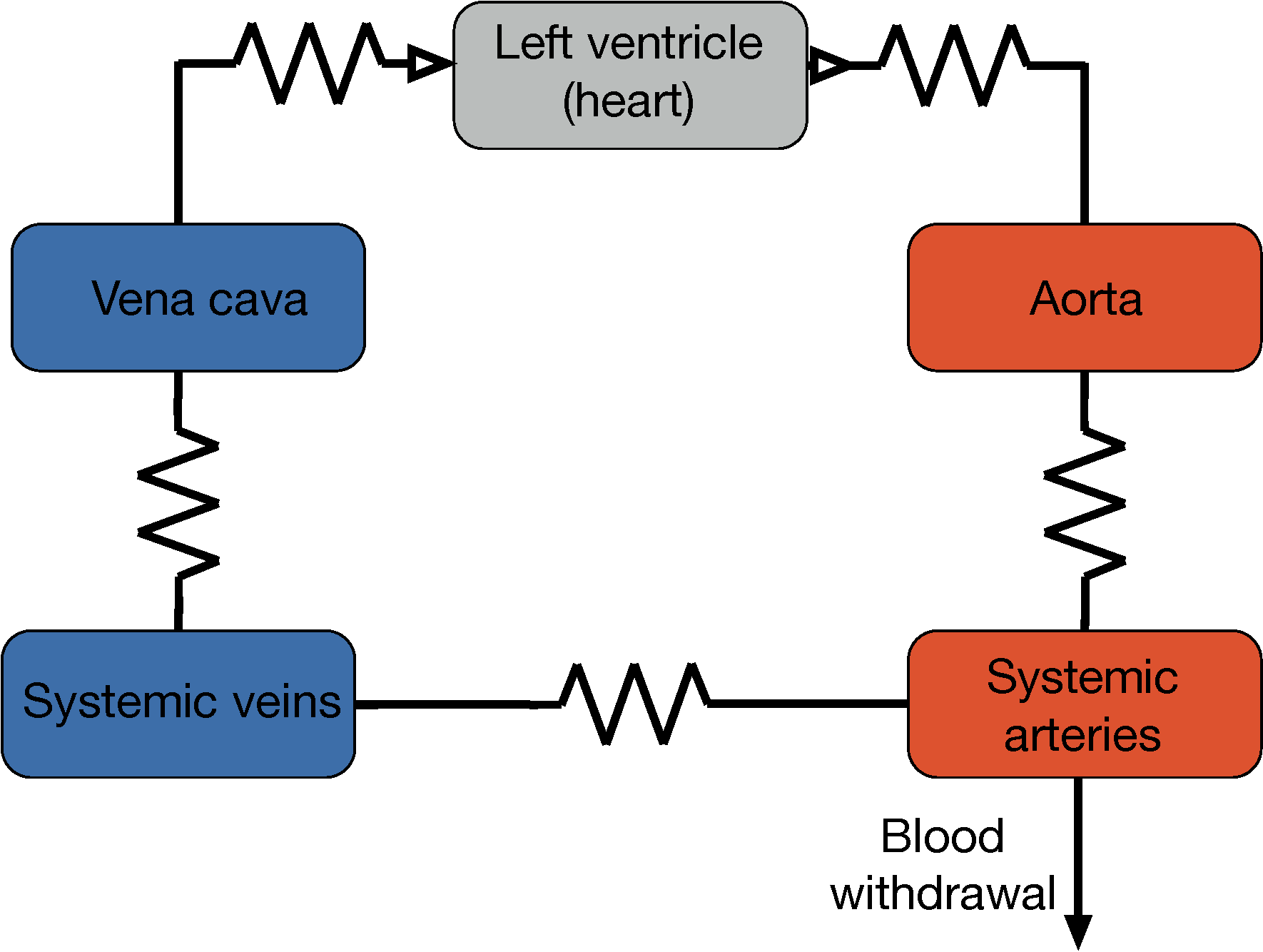
In the Mathematics Research Communities workshop in summer 2016, we started modeling mechanisms through which the cardiovascular system is able to return to normal pressure and volume following blood loss. Using improved calibrated left ventricular pressure and volume data, we are modeling key time-varying parameters such as left ventricular elastance and systemic resistance with differential equations to provide insight into how the baroreflex mechanism regulates heart pressure and volume. (See report.)

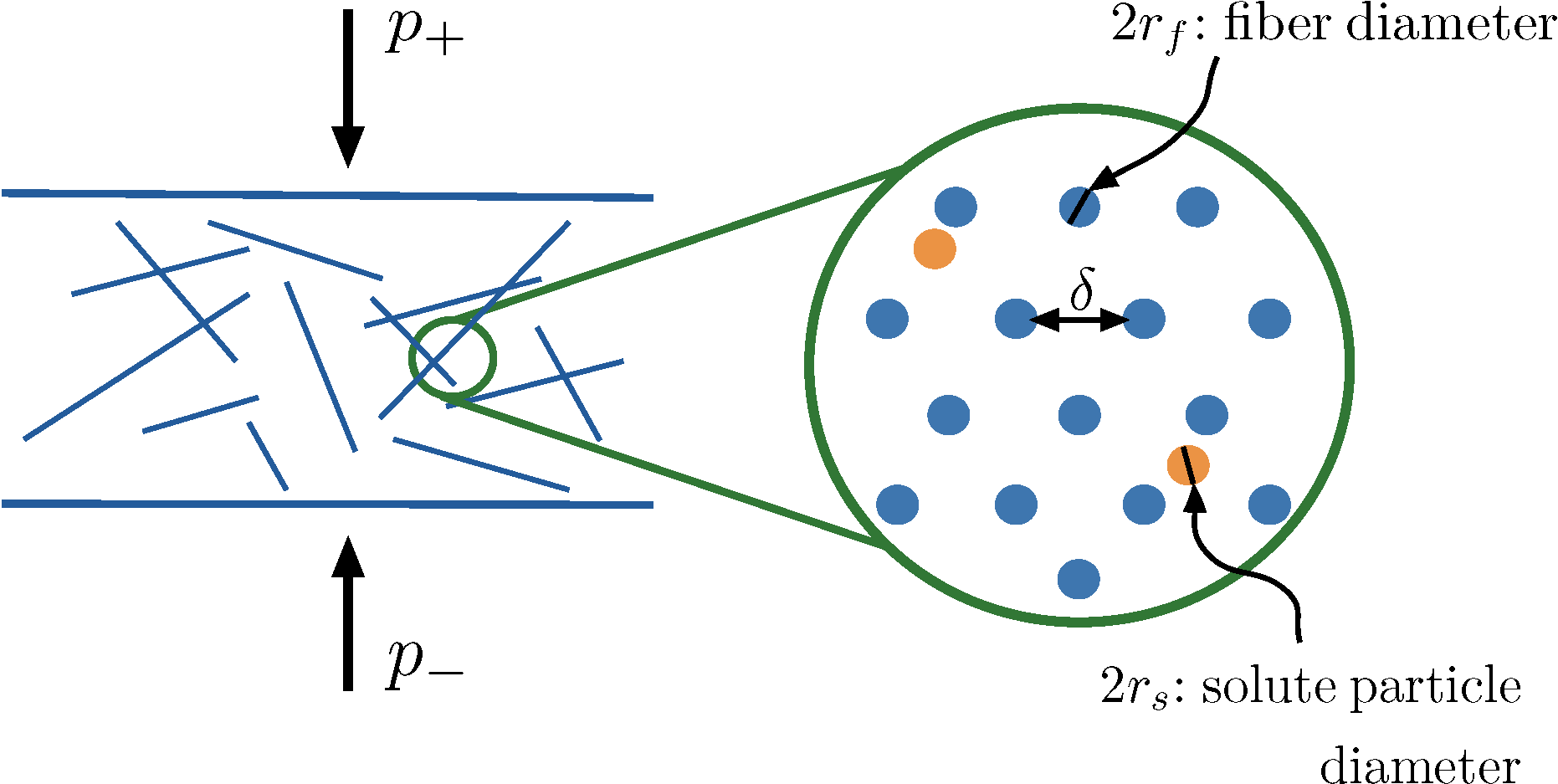
During the Mathematical Problems in Industry (MPI) Workshop in summer 2016, we started studying transport properties of membranes that are used to filter out solute from a fluid, in particular after membranes are rolled and compressed into cannisters. Our preliminary approach is to mathematically characterize a filter consisting of randomly oriented fibers using fiber matrix structure theory, and develop numerical methods predicting the concentration of solute after compression. (See report.)

In the 2015 REU project on Dynamics and Stochastics, we studied the impact of human interactions through home, social, and work/school contexts on the spread of influenza. We extended diary-based network data to larger networks of human interaction using context-specific methods. We then studied the spread of influenza on these extended networks and identified strategies that can lead to more effective suppression of disease spread.

Stability of agent-based models for zebrafish stripe formation

In the Summer @ ICERM 2016 REU program, we were interested in the stability of patterns arising in agent-based models, motivated by zebrafish stripe formation. We use the framework of piecewise-deterministic Markov processes (PDMPs) to account for deterministic and stochastic processes occurring on the same timescale in these models.
In preparation for submission to SIURO.

Collaborators: Cassandra Cole, Philip Doldo, Qing Fan, Alexandria Volkening, Björn Sandstede
Congratulations to Claire, Cassie and Philip for winning an Outstanding Poster Award in the Applied Mathematics category at the JMM Undergraduate Poster Session in January 2017!

Lead propagation in the body

In the Summer @ ICERM 2016 REU program, we studied lead accumulation in the body after decades from ingestion. We constructed ODE and PDE models and investigated the impact of nonlinearities and diffusion in modeling lead propagation.

Collaborators: Jordan Collignon, Melissa Morrissey, Todd Kapitula
Congratulations to Jordan and Melissa for their manuscript acceptance at SIURO in July 2017!

---

Reading Group

Dr. Sandstede's research group participates in weekly meetings each semester where we discuss topics in dynamical systems. The semesters and topics I participated in so far are listed below, along with the themes I covered in my group presentation each semester.

Semester:	Topic:	My subtopic:	Presentation (slides/notes):
Fall 2014	Traffic flow	Pedestrian traffic models	slides
Spring 2015	Dynamics of networks	Static networks: Structural properties of networks, Erdos-Renyi random graphs and connectivity properties	notes
Fall 2015	Microscopic versus macroscopic models	Large systems of interacting particles - paper presentation	slides
Spring 2016	Nonlinear waves: Spatial dynamics and Fredholm approaches	N/A	N/A
Fall 2016	Vegetation patterns	Pattern formation via amplitude equations (2 lectures) Barbier 2006: Self-organized vegetation patterns	outline slides
Spring 2017	Data science	Persistent homology / Topological data analysis	slides