Math & Beauty & Brain Areas
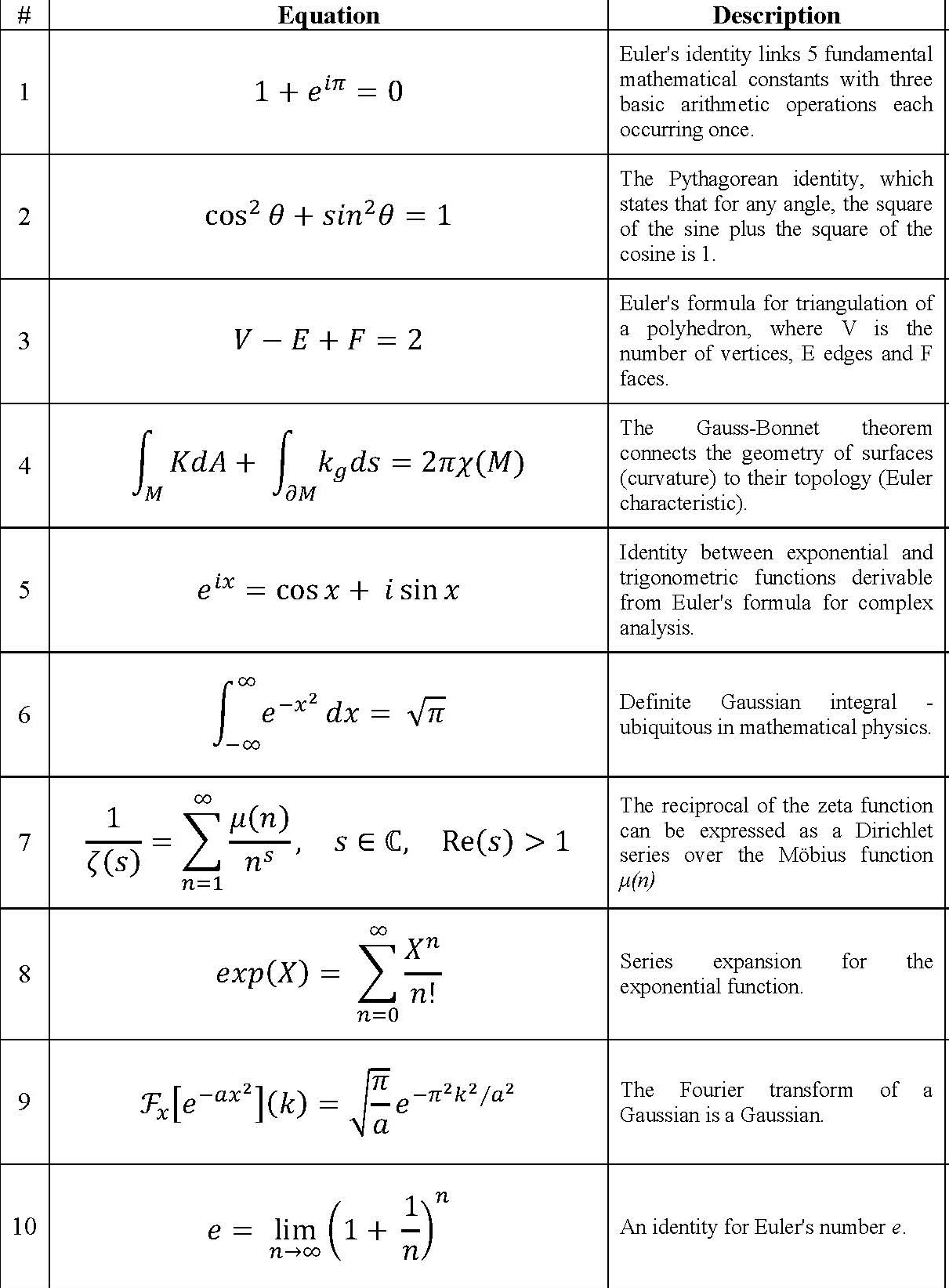
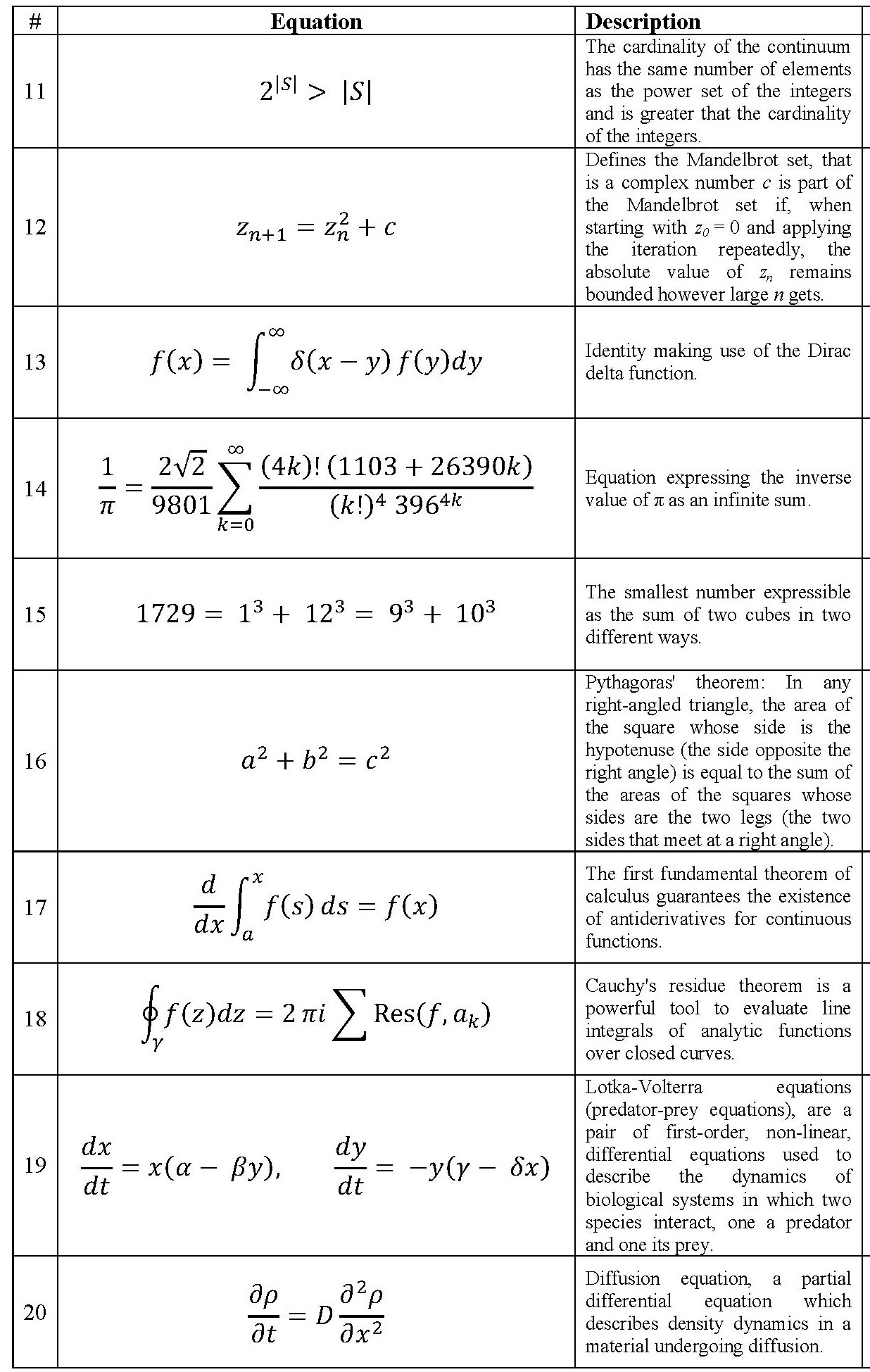
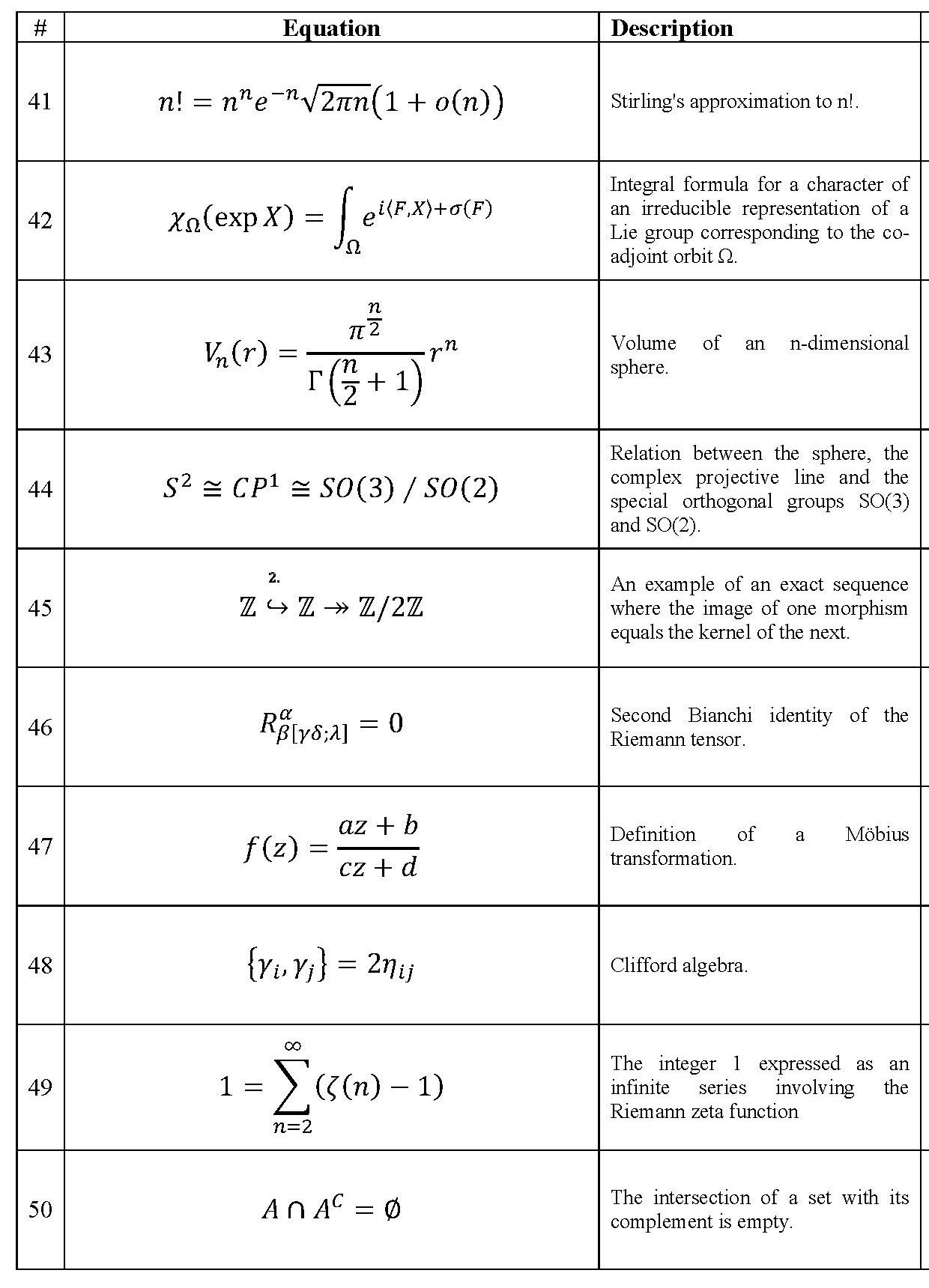
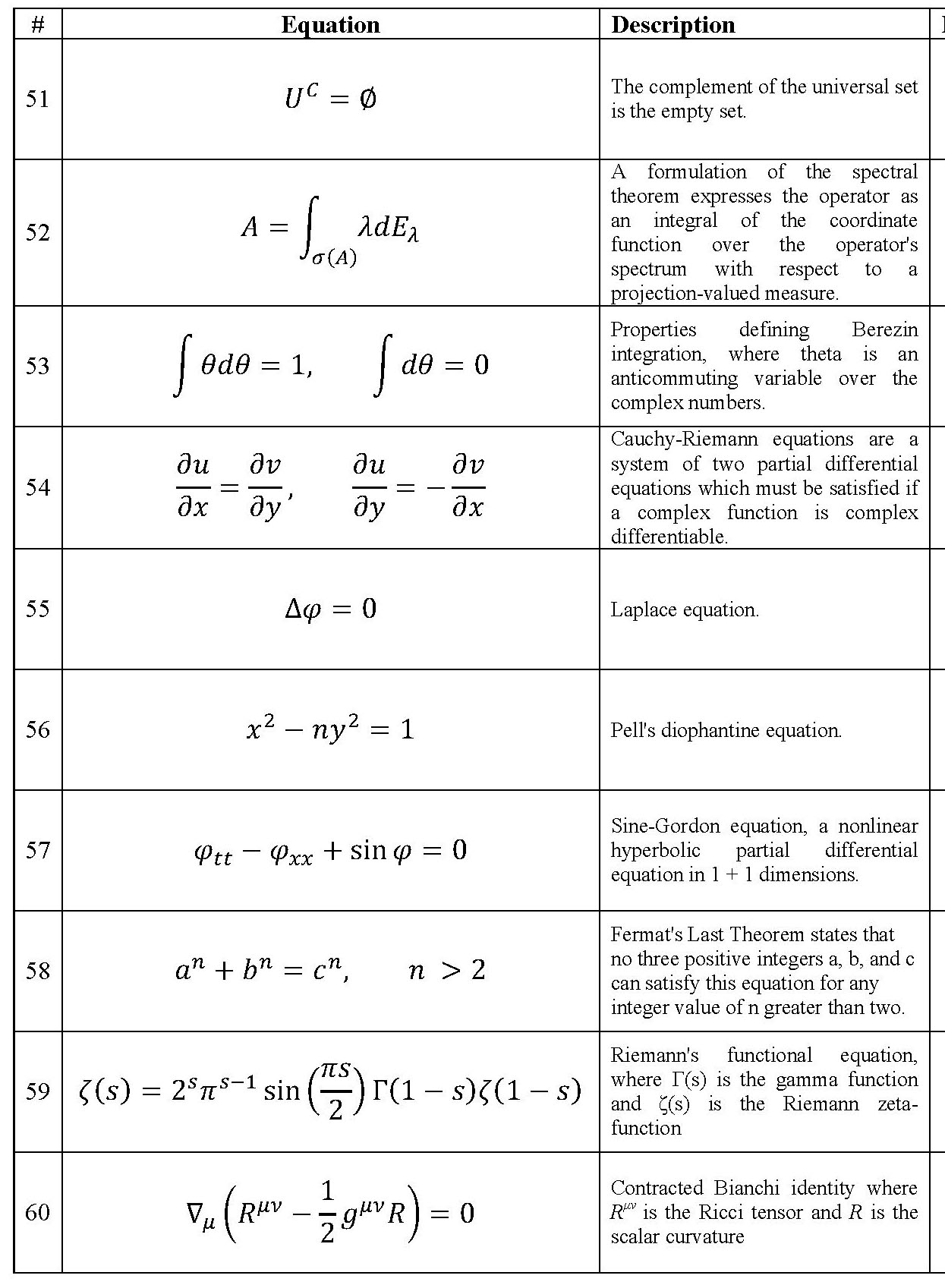
Two questions about the general nature of math have a certain interest to the larger public: mathematicians like to talk of a 'beautiful result' but what does this mean?; and is there a special part of cortex which is highly active when people do math? Recently Professors Michael Atiyah and Semir Zeki have put these two questions together, collaborating on an astonishing experimental investigation of these questions entitled "The experience of mathematical beauty and its neural correlates". Fifteen mathematicians were scanned using fMRI while viewing 60 mathematical formulas and rating them as ugly, neutral or beautiful. All 60 equations are shown in the sidebar, in 6 jpegs: you can magnify them by clicking. Their main result is that activity in the mOFC = medial (near the centerline) orbital (in the inward curl of the cortex above the eyes) frontal cortex correlates to some extent with their judgement of beauty (though strangely activity in mOFC relative to baseline diminishes). My aim in this post is to argue for the view that the subjective nature and attendant excitement during mathematical activity, including a sense of its beauty, varies greatly from mathematician to mathematician and that that would make it plausible for quite different parts of the brain to be active during mathematical reflection. I do not claim any scientific basis for this as my only evidence comes from opportunities to talk with colleagues and being struck with the remarkably diverse ways they seem to have of 'doing math'.
A word of apology before I get started: much of what i want to say is understandable to non-mathematicians, but, in order to make my case, I need to cite many specific mathematicians and mathematical results that are only clear to fellow mathematicians. I have included some background to make the ideas clearer to non-mathematicians but this is an uneasy compromise.
I think one can make a case for dividing mathematicians into several tribes depending on what most strongly drives them into their esoteric world. I like to call these tribes explorers, alchemists, wrestlers and detectives. Of course, many mathematicians move between tribes and some results are not cleanly part the property of one tribe.
Explorers: I want to give examples for each tribe of specific beautiful results and specific people I have known and interacted with in this tribe. Arguably the archetypal discovery by explorers was the ancient Greek list of the five Platonic solids: the only 'regular' convex polyhedra (meaning that any face and vertex on that face can be carried to any other such face, vertex pair by a rotation of the polyhedron). This discovery is sometimes attributed to Theaetetus, is described by Plato in the Timaeus dialog and worked out in detail in Euclid's Elements. I find it curious that nowhere, to my knowledge, is an icosahedron or a dodecahedron ever described in Indian or Chinese writings prior to the 17th century merging of their mathematical traditions with those of the West. Enlarging the mathematical universe from three dimensions to higher dimensions started a gold rush for explorers. In the 19th century, the Swiss mathematician Ludwig Schläfli extended the Greek list to regular polytopes in n dimensions, finding 6 in four dimensional space but only 3 in all higher dimensional spaces. In the 20th century, exploring all possible low dimensional manifolds (both homeomorphic, piecewise-linear and differentiable types) has been a major focus. I knew my contemporary Bill Thurston fairly well and he seems to me to have been clearly a member of the explorer tribe. He was a fantastic topologist and it was especially intriguing to me that he was born cross eyed, thus his understanding the 3D world was forced to depend more on parietal areas and hand-eye coordination than occipital cortex, stereo based learning. I never met anyone with anything close to his skill in visualization (except perhaps for H. S. M. Coxeter).
But explorers are not all geometers: the list of finite simple groups is surely one of the most beautiful and striking discoveries of the 20th century. Although he is not a card-carrying explorer, having devoted much of his career to detective work, in the second half of his career, Michael Artin discovered an amazing rich world of non-commutative rings lying in the middle ground between the almost commutative area and the truly huge free rings. "Rings" are sets of things that can be added and multiplied, but here he allows \( x\cdot y \ne y \cdot x \). He really set foot on a continent where no one had a clue what might be found: this exploration is ongoing. And then there is that most peculiar, almost theological world of 'higher infinities' that the explorations of set theorists have revealed.
My own career has been centered in the mapper sub-tribe. My maps are called moduli spaces of varieties (finite-dimensional objects) and moduli spaces of sub-manifolds of Euclidean spaces (infinite-dimensional objects). But one can make the case that the earliest members of the explorer tribe, even the earliest mathematicians, were literally mappers. I have in mind the story told by cuneiform surveying tablets. The earliest organized states in the world confronted the tasks of keeping track of land ownership and of taxing farmers. We are lucky to have a vast collection of Mesopotamian tablets from the late third millennium to the mid first millennium BCE. Many of these tablets contain idealized maps of land or of geometric constructions stimulated by surveying tasks. It seems fairly clear that the scribes who wrote these tablets went on to discover much of the geometric algebra, Pythagoras's rule and the quadratic equation as a result of being presented with practical land use and accounting challenges. They had no interest in questions of proof, only in algorithms related to measuring the earth, its distances and areas, (which they called the wisdom of the goddess Nisaba with her rope and measuring reed).
The Atiyah-Zeki list has very few results of explorers, perhaps because their results are not usually expressed by formulas. However, it contains three gems: #12, the Mandelbrot set; #15, an integer expressible two ways as a sum of two cubes, famous because Ramanujan told it to Hardy; and #28, the (3,4,5) right triangle. Another set of formulas selected this time by ten mathematical scientists is the Concinnitas project of Bob Feldman and Dan Rockmore of ten aquatints (the link is to my post and contains the formulas). It contains a gem from the short list of finite simple groups, here the groups discovered by Rimhak Ree. I would like to add that some of the things that gave me the most pleasure in my own research were discovering unusual previously unknown geometric objects: one was a negatively curved algebraic surface whose homology was the same as that of the positively curved \( \mathbb{P}^2 \) .
Alchemists: For many people, the most wonderful results in mathematics are those that reveal a deep relationship between two very distant subjects, for instance a link between algebra and geometry, algebra and analysis or geometry and analysis. Such links suggest that the world has a hidden unity, previously concealed from our mortal eyes but blindingly beautiful if we stumble upon it. An early example of such a link is the connection of the geometric problem of trisecting an angle and the algebraic problem of solving cubic polynomial equations. The first was one of the major unsolved problems of the ancient Greek tradition. In the Renaissance, Italian algebraists found a mysterious formula for the roots of a cubic polynomial. But in the case where all three roots are real, their formula led to complex numbers and cube roots of such numbers. The French mathematician Viète was the 'alchemist' who made the link c.1593: he showed how, if you can trisect angles, you can solve these cubic equations and vice versa. It wasn't until the early18th century, however, that another Frenchman, Abraham De Moivre really explained the result with his formula $$ (\cos(\theta)+i.\sin(\theta))^n = \cos(n\theta)+i.\sin(n\theta).$$ This is surely alchemy. But I would classify the leading mathematicians of the 18th and early 19th century, Leonard Euler from Switzerland and Carl Fredrich Gauss from Germany as the 'strip miners' who showed how two dimensional geometry lay behind the algebra of complex numbers. Euler's form of De Moivre's formula appears as #5 (and #1) of the Atiyah-Zeki list.
My PhD advisor Oscar Zariski was surely an alchemist. His deepest work was showing how the tools of commutative algebra, that had been developed by straight algebraists, had major geometric meaning and could be used to solve some of the most vexing issues of the Italian school of algebraic geometry. More specifically, the algebraic notions of integral closure and of valuation rings were shown to relate to geometry in Zariski's 'Main theorem' and his work on resolving singularities. He used to say that the best work was not that proving new theorems but that creating new techniques that could be used again and again.
The famous Riemann-Roch theorem has been an especially rich source of alchemy. It was from the beginning a link between complex analysis and the geometry of algebraic curves. It was extended by pure algebra to characteristic p, then generalized to higher dimensions by Fritz Hirzebruch using the latest tools of algebraic topology. Then Michael Atiyah and Isadore Singer linked it to general systems of elliptic partial differential equations, thus connecting analysis, topology and geometry at one fell swoop. Out of modesty, Atiyah did not include this in his list but he did put in its special case, the Hirzebruch signature formula, in his aquatint in the Feldman-Rockmore project. These aquatints also include the Dyson-MacDonald combinatorial formula for \( \tau(n) \), numbers which come from complex analysis: surely alchemy. Finally, a most bizarre formula for \( 1/\pi \) appears as formula #14 in the Atiyah-Zeki list. I suspect this was included by the authors because they suspected that many would think it ugly. I have no idea where it comes from but whoever found it belongs to the sub-tribe of Baroque Alchemists. It stands in contrast to the much simpler but nonetheless alchemical formula #30 for \( \pi \).
Wrestlers: Wrestling goes back to Archimedes: he loved estimating \( \pi \) and concocting gigantic numbers. The very large and very small have always had a fascination for wrestlers. Calculus stems from the work of Newton and Leibniz and in Leibniz's approach depends on distinguishing the size of infinitesimals from the size of their squares which are infinitely smaller. A laissez-faire attitude towards infinities and infinitesimals dominated the 18th century, resulting in alchemy gone amuk as in Euler's really strange formulas: $$ \frac{1}{2} = 1-1+1-1+1- \cdots, \quad \frac{1}{4}=1-2+3-4+5-\cdots$$ Of course Euler knew these only made sense when viewed in a very special way and he himself had not gone crazy. In fact, many might say the above are very beautiful formulas. A notable much more understandable achievement of wrestlers in this century was Stirling's formula for the approximate size of n! (#41 in the Atiyah-Zeki list). The modern father of the wrestling tribe in the 19th century should be the Frenchman Augustin-Louis Cauchy who finally made calculus rigorous. His eponymous inequality, that the absolute value of the dot product of 2 vectors is less than the product their lengths, $$ |(\vec x \cdot \vec y)| \le \|\vec x\|\cdot \|\vec y\| $$ remains the single most important inequality in math. Atiyah-Zeki include the related triangle inequality as #25.
I was not trained as a wrestler but I, at least, had a small education later because of my work in applied math. I did fall in love with the wonderful inequalities of the Russian analyst Sergei Sobolev. The simplest of these illustrates what many contemporary wrestlers deal with: say f(x) is a smooth function on the real line. Then for all a,b, one has the simple Corollary of Cauchy's inequality: $$ |f(b)-f(a)|^2 \le |b-a| \cdot \textstyle\int ( \tfrac{df}{dx} )^2 dx.$$ Thus one says that a square integral bound on the derivative "controls" its point wise values. When I was teaching algebraic geometry at Harvard, we used to think of the NYU Courant Institute analysts as the macho guys on the scene, all wrestlers. I have heard that conversely they used the phrase 'French pastry' to describe the abstract approach that had leapt the Atlantic from Paris to Harvard.
Besides the Courant crowd, Shing-Tung Yau is the most amazing wrestler I have talked to. At one time, he showed me a quick derivation of inequalities I had sweated blood over and has told me that mastering this skill was one of the big steps in his graduate education. Its crucial to realize that outside pure math, inequalities are central in economics, computer science, statistics, game theory, and operations research. Perhaps the obsession with equalities is an aberration unique to pure math while most of the real world runs on inequalities.
Other examples of wrestler's work in the Atiyah-Zeki list are #11 (Cantor's inequality); #26 (the prime number theorem); and #38 (convexity of logs).
Detectives: Andrew Wiles said he worked on Fermat's claim that \( x^n + y^n = z^n \) has no positive integer solutions if \( n \ge 3 \) obsessively for eight years, describing the work as follows (in this PBS interview ):
I used to come up to my study, and start trying to find patterns. I tried doing calculations which explain some little piece of mathematics. I tried to fit it in with some previous broad conceptual understanding of some part of mathematics that would clarify the particular problem I was thinking about. Sometimes that would involve going and looking it up in a book to see how it's done there. Sometimes it was a question of modifying things a bit, doing a little extra calculation. And sometimes I realized that nothing that had ever been done before was any use at all. Then I just had to find something completely new; it's a mystery where that comes from. I carried this problem around in my head basically the whole time. I would wake up with it first thing in the morning, I would be thinking about it all day, and I would be thinking about it when I went to sleep. Without distraction, I would have the same thing going round and round in my mind. The only way I could relax was when I was with my children. Young children simply aren't interested in Fermat. They just want to hear a story and they're not going to let you do anything else.Although this is extreme, this sort of pursuit is well known to all mathematicians. The English mathematical physicist Roger Penrose once described his way of working similarly: "My own way of thinking is to ponder long and, I hope, deeply on problems and for a long time ... and I never really let them go." In many ways this is the public's standard idea of what a mathematician does: seek clues, pursue a trail, often hitting dead ends, all in pursuit of a proof of the big theorem. But I think it's more correct to say this is one way of doing math, one style. Many are leery of getting trapped in a quest that they may never fulfill. Peter Sarnak at the Princeton Institute for Advanced Study has described what it feels like to be a research mathematician by the sentence "The steady state of a mathematician is to be blocked". Arguably Landon Clay may have done maths no service by singling out seven of the deepest, most difficult math problems and putting a million dollar bounty on each. Putting a dollar value on a proof is quite bizarre and the prize was declined by Grigori Perelman, the only winner in this contest so far. In any case, I believe it is more common among mathematicians to become intimately familiar with a range of related problems while not necessarily actively working on any of them. But these problems are not far from their consciousness and from time to time, a clue will show up, a hint of some connection, and then it all rushes back and hopefully some progress is made on one of the problems.
Among those who attack major problems, a very small number are able to imagine a deeper more abstract layer of meaning in the problems of the day, that others never imagined.They are detectives who feel the answer is deeply hidden, so you need to strip away all the features of the situation that are accidental and thus irrelevant to understanding it. Underneath you find its true mechanisms, what makes it tick. It seems only logical to call such people strip miners, though not in a pejorative sense. The greatest contemporary practitioner of this philosophy in the 20th century was Alexander Grothendieck. Of all the mathematicians that I have met, he was the one whom I would unreservedly call a "genius". But there have been others before him.
I consider Eudoxus and his spiritual successor Archimedes to be strip miners. The level they reached was essentially that of a rigorous theory of real numbers with which they are able to calculate many specific integrals. Book V in Euclid's Elements and Archimedes The Method of Mechanical Theorems testify to how deeply they dug. Some centuries later and quite independently, Aryabhata in India reached a similar level, now finding what are essentially derivatives, fitting them into specific differential equations. But it is impossible to fully document the achievements of either of these mathematicians as only fragments of their work survive and there is no way to reconstruct much of the mathematical world in which they worked, the context for their discoveries. Grothendieck's ideas, however, and world both before and after his work are very clearly documented. He considered that the real work in solving a mathematical problem was to find le niveau juste in which one finds the right statement of the problem at its proper level of generality. And indeed, his radical abstractions of schemes, functors, K-groups, etc. proved their worth by solving a raft of old problems and transforming the whole face of algebraic geometry. Mike Artin, John Tate and I have documented four of his greatest successes in the obituary to appear in the Notices of the AMS (forthcoming, early 2016). Pretty wonderful French pastry.
Many of the formulas in the Atiyah-Zeki list seem to me to come from the Baptismal tribe. #10 defines e; #13 defines the \( \delta \)-function; #21 defines \( \pi \); #24 defines eigenvectors; #47 defines Möbius maps; #48 defines Clifford algebras. I have not mentioned many of the remaining equations in the Atiyah-Zeki list. It seems to me that many are intermediate results in a developing theory, found by detectives doing great work. It is hard for me to judge which are more beautiful: their attraction comes from their bringing to mind a whole beautiful theory of which they are one part. For instance, #36, \( \langle B,B \rangle_t = t \) , the variance of Brownian motion, is hugely important and beautiful but I would think of it as a natural consequence of the more basic fact that, when you add independent random variables x and y, their standard deviations follow the stochastic version of Pythagoras's rule.: $$ \text{St.Dev.}(x+y) = \sqrt{ (\text{St.Dev.}(x))^2 + (\text{St.Dev.}(y))^2}$$
Brain areas for the different forms of beauty?: It is clear that members of each tribe will make different judgements on the relative beauty of specific mathematical formulas or theorems. I want to take up each one in turn and ask what cortical activity they might produce. Explorers clearly find a tremendous thrill in the Systema Naturae, the flora and fauna and gazetteers produced by their explorer colleagues. Exotic creatures like non-standard differential structures on Euclidean 4-space continue to amaze and to defy visualization. But I suspect that geometers have mental tricks that allow them to piggy-back a sense for high dimensional constructions on top of their 3-dimensional skills. Thus constructions like surgery and suspension can be visualized in the simplest cases and the mind builds the skills that allow the general case to be grasped as an analog of these. I remember Zariski, getting stuck at a certain point in his lectures, drawing a bit of an algebraic plane curve (a cubic with a double point) in the corner of blackboard to kickstart his intuition. Steve Kosslyn and others have studied cortical activity with fMRI while a subject is forming a visual mental image of some object (here is one reference). There seems to be a complex pattern of widespread activity -- frontal as well as parietal and temporal -- as well suppression of activity in what I guess is pretty close to Zeki's mOFC (see the blue area in the top row in the figure on p.231 of the cited paper). But people who are not geometers may never use visualization in their research. There's a probably apocryphal story about the algebraist Irving Kaplansky: asked what he saw when you asked him to think about a ring replied "I see the letter 'R' ".
The most common 'beautiful' formulas are alchemical. The famous: $$ e^{i\pi} = -1$$ brings together exponential growth with the geometry of the circle. When a formula connects two concepts that would seem to have absolutely nothing to do with each other, you get a chill running down your back. It feels as though the universe wasn't forced to be this way so it is not unreasonable to ask God "why did you decide to make this happen?". In other words, it is hard to dispel a sense of mystery that clings to them. Is there an area of the brain which is active when you can't figure out why something happened, when you are mystified by some event? It would seem hard to devise fMRI experiments to find such a "mystery-center". But I believe that alchemists find the greatest beauty in such mysteries.
What is going on in the minds of wrestlers? My guess is that estimating size and relative power of math things is connected to our social behavior, to Darwinian selection of the fittest. Animal life is all about being strong enough to get the stuff you need. A large number of species exists in a hierarchical social setting, with each individual learning rapidly whom to defer to, whom to dominate. And Robin Dunbar has shown that the size of your working social group goes up exponentially with your brain size, thus humans must have large cortical areas devoted to deeply understanding the interactions of their large groups -- he estimates that on average each person lives in group of some 150 people whom "you wouldn't feel embarrassed about joining for a drink if you happened to bump into them in a bar". Although I haves not seen any experiments with this focus, I feel there must be cortical areas specialized for learning social structures and the complex web of pair relationships it contains. (Perhaps anterior cingulate cortex?) Given how central this is in our brains and lives, it feels to me that when structuring math objects, especially functions, by size (rate of growth, degree of smoothness, etc.), you would utilize this machinery built in for creating social hierarchy. I don't mean that you personify these math sizes, but only that making a partially ordered graph like structure is a skill you already have because of evolution.
Solving a puzzle is the basic drive for the detective tribe and the goal that gives them the greatest pleasure. In this case, there need not be a beautiful formula that encapsulates the solution. Rather, the proof itself is wonderful and beautiful. (Confession: I personally find quite stupid puzzles like Sudoku rather addictive.) This is surely a central aspect of pre-frontal activity: planning your activities is finding a path in a world satisfying many constraints that leads to some desired goal. Math is, however, a bit different from the world: if you are trying to prove a theorem, you have to be prepared to reverse course and prove its negation. Never put all your money on one result. Perhaps, way out the imaginary axis, the Riemann zeta function does have a zero with real part not equal to 1/2.
Summarizing, I see visualizing an alien abstract world, finding new mysteries, creating vast hierarchies or solving the hardest puzzles as four aspects of what mathematicians find most beautiful. But each has its characteristic form of beauty that connects it to distinct parts of our mental life. Can we expect to nail each down to a specific part of the brain? Recall that most of the qualities localized in 19th century phrenology have long since not been dropped as labels for specific cortical areas. The perception of mathematical beauty may also turn out to be a higher order derivative phenomenon characterized by patterns of activity widely distributed over the brain.
I've had a few emails relevant to this post. Andrew Solomon writes:
I like Freeman Dyson's Bird/Frog taxonomy, sort of meta to yours. Also the "Beauty is truth,truth beauty" quote is perhaps relevant if one considers, as I do, that the only real truth is math. (Not that I know much about it, but I'm sure that categorical surmise would take a lot of heat, especially if math is perceived as reliant on axioms.) Lastly, while you elegantly articulate the various thought processes that go into math thinking in your tribal division, I would say that resolution might be lost when simply looking at the equations under consideration. I wonder how much visual accessibility determines voting in comparison to the math lying behind a given equation. Similarly, what is the influence of sentiment, e.g., when considering (what might be considered an inside joke) Hardy's taxi number.
And my good friend and once student Ulf Persson also focussed on the issue of "visual accessibility" by rewriting \( e^{i\pi}=-1 \) :
What about m1_eq3PV)(Mo/? Is that a beautiful formula? This brings up the perhaps trivial issue of beauty being perhaps also in the visual sense of the formula, not only its mathematical contents. When artists try to write mathematical formulas, they use a lot of square roots signs. Maybe those are the most visually striking elements. I recall how intrigued I was by the formulas in Hardy's 'Pure Mathematics', in particular the partial derivative signs intrigued me, and would do so even when I had become mathematically literate. As to the initial formula, this is an amalgam of old notations. Thus 'm' for minus eq for equality, now P should mean taking the power of what preceded it, in this case 3, and V indicates that everything that comes after should be included in the exponent . (Cardano used V in RV to indicate that anything came after would be taken the square root of). Finally the Greeks used Greek letters to designate numbers, Diophantine dotted them when they should be taken literally as their numerical values. Thus 1_, while 3 is thought of as a letter to designate e. The imaginary i is given by )( to emphasize its imaginary nature, M is of course multiplication and o/ should obviously denote pi. There is something to be said for streamlined notation. The point of algebraic notation, as I tell my students, is not just to encode information, but more important to be able to manipulate it easily.
And another good friend, also once a student, Larry Gonick (the author of mathematical, scientific and historical cartoon textbooks) wrote me how the "visual accessibility" of Dan Rockore's series of formulas continues to intrigue the art world (!):
I've been meaning to write since we saw the equation prints at the Crown Point Press opening two weeks ago. Yours I thought the handsomest of the lot, though a couple of integral signs had some swash. The Press put your image on the post card. Sample available upon request. The discussion, as you may imagine, was a little strange. The head of the press put herself and her husband on a panel with Dan Rockmore and Dick Karp from Berkeley. All were good talkers, but the artists knew zero about math (and they spoke first, at great and aimless length). Afterward, I had the definite impression that some art groupies were flinging themselves at Dan. See what you missed?