The lowest zeros of Riemann's zeta are in front of your eyes
Barry Mazur and William Stein are writing an excellent book entitled What is Riemann's Hypothesis? The book leads up to Riemann's 'explicit formula' which, in von Mangoldt's form, is the formula for the discrete distribution supported at the prime powers: $$ \sum_{\text{primes }p} \sum_{n \ge 1} \log(p) \delta_{p^n} (x)= 1 - \sum_k x^{(\rho_k-1)} - \tfrac{1}{x(x^2-1)} $$ where \( x > 1 \), \(\rho_k \) ranges over the zeros of the zeta function in the critical strip \( 0 < \text{Im}(\rho) < 1\) and the sum over k converges weakly as a distribution. This relates primes to the zeta zeros. In this blog, I ask: can we find the first and maybe more low zeroes hidden in the very smallest primes?
Riemann called the terms in \(\rho_k\) the oscillating terms because if \( \rho_k = 0.5 + i.\omega_k \) and we pair symmetric roots \( \pm \omega \), then $$ \sum_k x^{\rho_k-1} = 2\sum_k \cos(\log(x).\omega_k) / \sqrt{x}.$$ Thus Riemann showed that the logs of the primes show periodic behavior. Let's start from scratch and ask if we find periodic behavior in the logs of the smallest primes or, as they get larger, clusters of primes.
The ratios of the lowest primes 2, 3, 5, 7, 11 are roughly 1.5, 1.67,1.4,1.57 which all cluster around 1.55. But then 13/11 is only about 1.18. To fix this, after 10 we shift from single primes to prime pairs, replacing the pair by the even number in the middle, getting the new sequence:
2, 3, 5, 7, 12 for (11,13), 18 for (17,19), 23?, 30 for (29,31), 37?, 42 for (41,43), 47?.
Skipping the isolated primes 23 and 37, the ratios are now 1.5,1.67,1.4,1.71, 1.5,1.67,1.4. If you make a linear fit to the logs, you find the sequence is approximated by $$ 1.27\cdot (1.557)^n \approx 1.98, 3.08, 4.80, 7.47, 11.64, 18.12, 28.22, 43.94. \cdots $$ Hmm: not bad. Also note that we ignored prime powers, which explains why the prime 5, dragged down by 4 became 4.8 and the prime 7, dragged up by 8 and 9, became 7.47. Even more startling, this power law would come from a periodic term in log-prime density of form \( \cos(2\pi \log(x)/1.557 \) and \( 2\pi/\log(1.557) = 14.185... \), which is very close to the first zero of Riemann's zeta, namely 14.1347...! In other words, the basic idea behind Riemann's periodic terms is indeed apparent in these small primes. This is especially startling because the convergence of the explicit formula is very slow: there are very many slowly oscillating terms beyond the first one so there is no compelling reason why the lowest \( \omega_k \) should nail these primes this well. Let's go back to the explicit formula and change coordinates to \(y=\log(x) \). Again writing the zeros as \( (0.5+i.\omega_k) \) where \( \omega_k \) is real under the Riemann hypothesis, being careful with the deltas and summing only over k with \( \omega_k > 0 \), you get:
$$ \sum_{p, n} \tfrac{\log(p)}{p^{n/2}} \delta_{\log(p^n)}(y) = e^{y/2} - 2\sum_k \cos(y\omega_k) - \tfrac{1}{e^{y/2}(e^{2y}-1)} $$
Note that instead of thinning out logarithmically as the primes do, the logs of primes now get dense at an exponential rate. After weighting the prime powers as shown, they still have density \( e^{y/2} \), the first term on the right. But after that we get oscillations. Curiously an immense amount of work has been done on very large primes and very large zeta zeros while this formula for small values of y doesn't seem to have been looked at. Let's first look graphically at the small log-prime-powers weighted as in this formula.
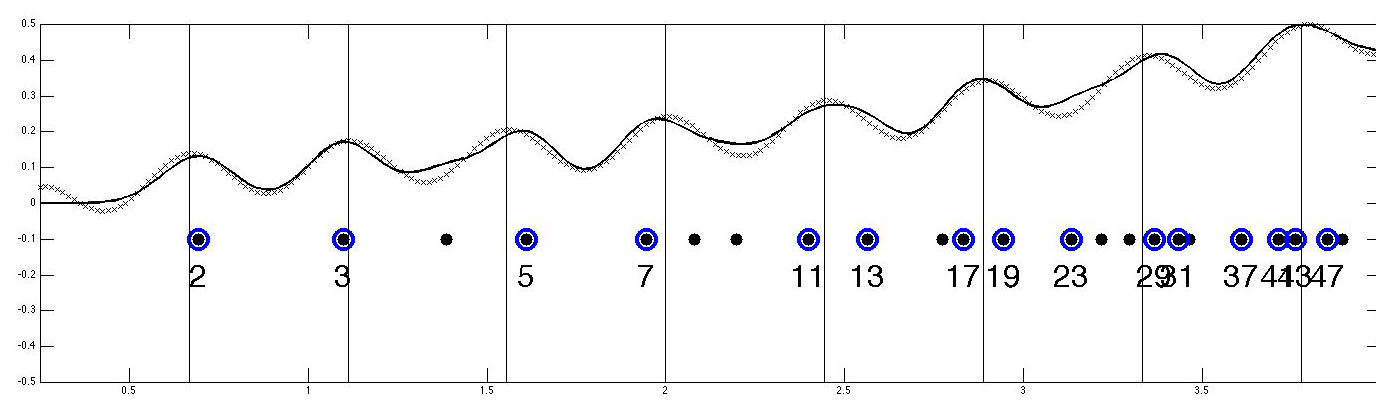 The horizontal axis is log scale, the filled circles are the logs of the primes up to 50, the dots the prime powers. The solid line is the convolution of the weighted sum of deltas as above with a Gaussian with standard deviation 0.1. The line of hatch marks is its approximation with the above explicit formula but using only ONE zero of zeta and the vertical lines are its peaks where the cosine equals -1. Note that 23 and 37 are being ignored and will require the next zero of zeta as will separating 5 and 7 from adjacent prime powers.
The horizontal axis is log scale, the filled circles are the logs of the primes up to 50, the dots the prime powers. The solid line is the convolution of the weighted sum of deltas as above with a Gaussian with standard deviation 0.1. The line of hatch marks is its approximation with the above explicit formula but using only ONE zero of zeta and the vertical lines are its peaks where the cosine equals -1. Note that 23 and 37 are being ignored and will require the next zero of zeta as will separating 5 and 7 from adjacent prime powers.
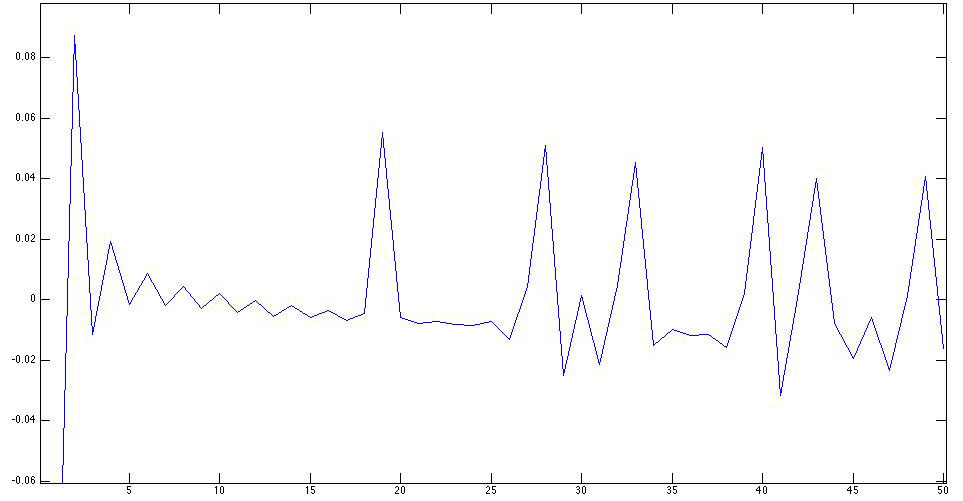
How many of the zeta zeros are hidden in the primes up to 53? Let's sample the interval [0,4] in the log-prime line discretely so we have deltas that are functions and take the discrete cosine transform. We find chaos in the high frequencies but terms \( cos(\pi \log(p) (k-1)/4) \) for \( 1 \le k \le 50 \) seem to be coherent and give us oscillating terms whose discrete frequencies correspond to
$$ \omega = 14.1, 20.0, 25.0, 30.4, 32.9, 37.6 \pm 0.4 $$
that are quite close to the true zeros 14.1, 21.2, 25.1, 30.6, 33.0 and 36.9. Below is the low frequency part of the DCT:
Can we find the oscillations in larger primes? The simple answer is that they get drowned in the exponentially increasing density of log-primes. Extending the above plot to higher primes, one finds that the slope of the large exponential function erases the local minima apparent for the small primes. There are several ways to find them however. One can simply subtract the mean density \( e^{y/2} \) or one can convolve the weighted sum of deltas with a suitable filter that kills the average. An engineer knows how to form filters that not only do this but also pick out some range of frequencies. This can be used to find the oscillations caused by all the zeros of zeta.
Let's stick to the simplest case. If we want to kill a constant term and suppress higher frequencies, a simple way is to convolve with the second derivative of the Gaussian. But we want to kill \( e^{y/2} \), so we need to first premultiply by \( e^{-y/2} \), then convolve with the second derivative and finally multiply back by \( e^{y/2} \). In one step, this amounts to convolving with:
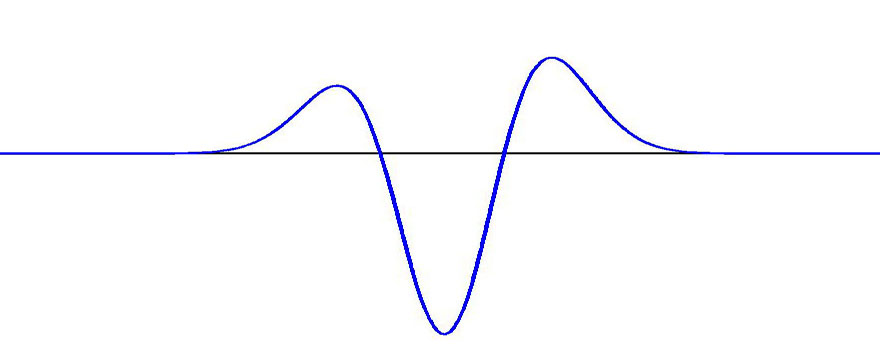
$$ (y^2 - \sigma^2)\cdot e^{-\frac{1}{2\sigma^2}(y-\frac{\sigma^2}{2})^2}. $$
For \( \sigma = 0.2 \), the value we will use, this kernel looks like this:
If we use this filter and convolve the weighted sum of deltas at the logs of all prime powers up to 3 million, we finally get:
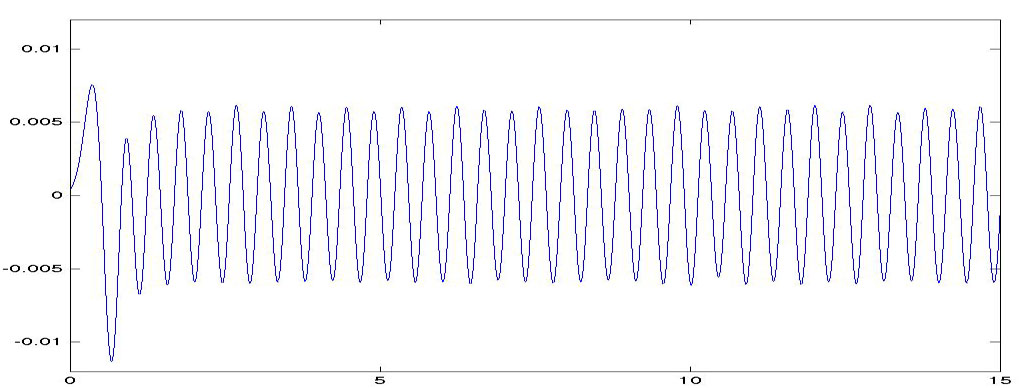 There are peaks for example around 1.9 million and around 3 million. I don't know if anyone has noticed this extra density of primes around these values. Note that we are not looking at one precise value but at a range, e.g. 1.75 million to 2.1 million and comparing it to a dip before and after. One wonders whether Gauss noticed this during his numerical exploration of \( \pi \).
There are peaks for example around 1.9 million and around 3 million. I don't know if anyone has noticed this extra density of primes around these values. Note that we are not looking at one precise value but at a range, e.g. 1.75 million to 2.1 million and comparing it to a dip before and after. One wonders whether Gauss noticed this during his numerical exploration of \( \pi \).
As Barry asked me, the fact that the lowest zeros of zeta show themselves in the very smallest primes seems to extend to Dirichlet L-series too. The simplest case is the mod 4 series, giving the sign +1 to primes congruent to 1 mod 4, and -1 when congruent to 3 mood 4. In fact, just as the lowest zero of Riemann's zeta is close to 2pi divided by the log of the ratio of the two lowest primes 3 and 2, the lowest zero of the L series (6.02) is close to \( \pi \) divided by the log of the ratio of 5 and 3 (6.15). This is because 5 and 3 are the two lowest odd primes and they have opposite residues mod 4, hence should differ by \( \pi \), not 2\( \pi \), in the oscillation caused by this zero.
Here's the plot, convolving the signed and weighted sum of deltas with a Gaussian of standard deviation 0.2.:
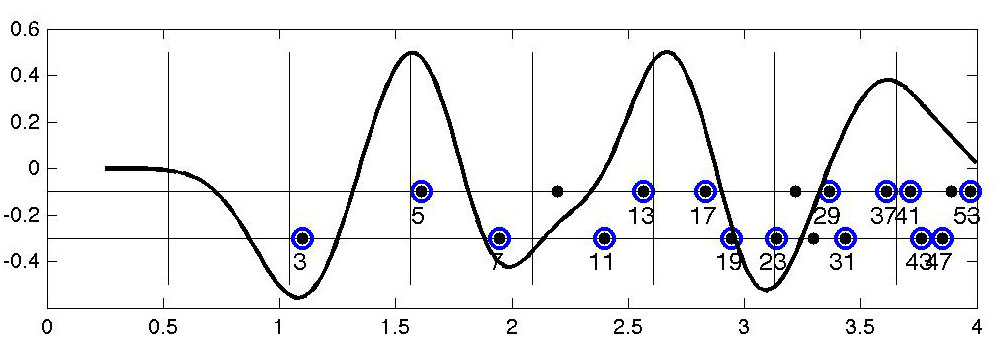 Note how we have negative peaks at 3, 7 and the pair [19 23], all congruent to 3 mod 4, and a positive peaks at 5, the pair [13 17] and the pair [37 41], all congruent to 1 mod 4. The vertical lines are half periods of the lowest frequency L-function oscillating term.
Note how we have negative peaks at 3, 7 and the pair [19 23], all congruent to 3 mod 4, and a positive peaks at 5, the pair [13 17] and the pair [37 41], all congruent to 1 mod 4. The vertical lines are half periods of the lowest frequency L-function oscillating term.