Works on Mathematics Education
My experience working in both pure and applied mathematics has given me a strong belief that, for almost all people, math is best learned first in the context of authentic applications and only afterwards, abstracted to a general setting. Moreover, a relatively small percentage of high school students will specialize in 'STEM' (Science, Technology, Engineering and Mathematics) professions and they can learn this in electives with more heavy duty math. I ask: how many quadratic equations do 99% of US citizens ever solve? Most students will benefit instead from applications that will actually be used in their adult lives. I've tried to argue for this approach in a variety of settings.
- Contributor to Multi-variable Calculus, The Calculus Consortium based at Harvard, Wiley, 1995. This was part of the major NSF sponsored "reform" initiatives of the 90's, this one being spear headed by Deborah Hughes-Hallett. The first version of this book was concise and clear and then the publishers demanded that all sorts of useless crap (e.g. drilling on rarely used techniques of integration) be added to make the book saleable.
- Calculus Reform -- For the Millions, Notices Amer. Math. Soc., May 1997, pp. 559-563.
Link to Notices OR Digital reprint. - Mathematics Belongs in a Liberal Education, The Arts and Humanities in Higher Education, 5, 2006, pp.21-32.
Digital reprint - How to Fix Our Math Education (with Sol Garfunkel), OpEd contribution to New York Times, August 25, 2011.
Digital reprint - Bottom Line on Math Education (with Sol Garfunkel), Huntington Post Blog, Nov. 30, 2011.
Link to Huffington Post OR Digital reprint - What's Really Wrong with Math Education -- and How to Fix It (with Sol Garfunkel). Rejected by a well known intellectual monthly but here's the manuscript .
- Teaching mathematics to serve the majority of 21st century American students (with Heather Dallas). Rejected by the NCTM but here's the manuscript One of our points was suggesting that teaching simple computer programming is a good 21st century replacement for the old "2-column" proofs in Euclidean geometry: both need attention to detail and careful analysis of sequencing steps. I was pleased just now to see that Jordan Ellenberg agreed, (more or less) and that his blog post generated a lot of comments.
- Some time ago, Klaus Peters published as a slim chapbook the wonderful essay of Hans Magnus Enzensberger "Drawbridge Up" and asked me to write a short preface. The ideas seem still relevant in this age of the "Common Core". Here it is:
I am accustomed, as a professional mathematician, to living in a sort of vacuum, surrounded by people who, as in the first paragraph of Enzensberger's essay, declare with an odd sort of pride that they are mathematically illiterate. How astonishing to come to the International Congress and find a distinguished poet and essayist who analyzes this problem with such a deep understanding and sensitivity. This is a beautiful essay and great delight for a mathematician to read. Here the strange contradictions with which we live are laid bare with accuracy of a dissecting microscope. He is onto our schizophrenic world in which, with one hand, we take pride in building an elegant world utterly divorced from the demands of reality and, with the other, claim that our ideas underlie virtually all technological developments of significance. I was particularly pleased to find that he believes progress is possible in teaching mathematics, that it can be made exciting to young minds. I tried (unsuccessfully) to get each high school in which my children were enrolled to go outside during geometry class and find out how tall the oak in the yard really is. Instead they buckled under to the establishment and even removed that staple of my generation: the odd formulaic Euclidean-style proof in which the pedigree of each step was detailed. This old game, the one piece of high school mathematics often mentioned warmly by people who otherwise hated math, had been found wanting by the mathematical puritans described in the Stewart quote, where the mathematician is unwilling to "lie a bit, like everyone else does". I hope the right people read this essay -- the movers and shakers of school curricula -- and that it moves them to let a hundred flowers bloom in the classroom.
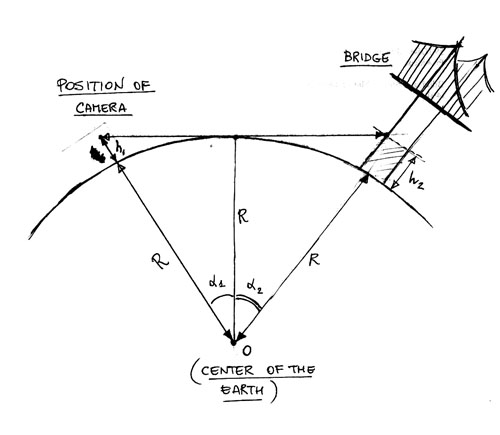 Diagram of the experiment
Diagram of the experiment  My photo of the Newport bridge 18 miles down the bay..
My photo of the Newport bridge 18 miles down the bay..