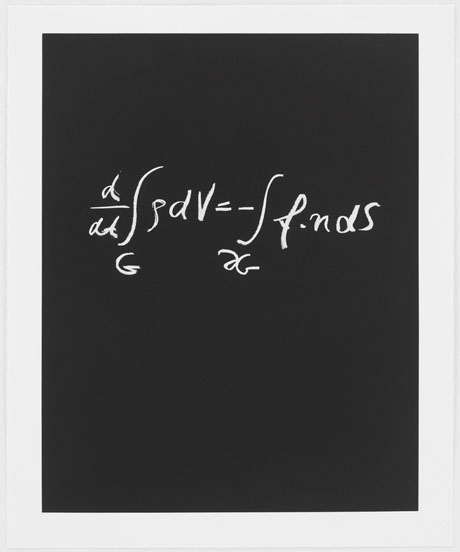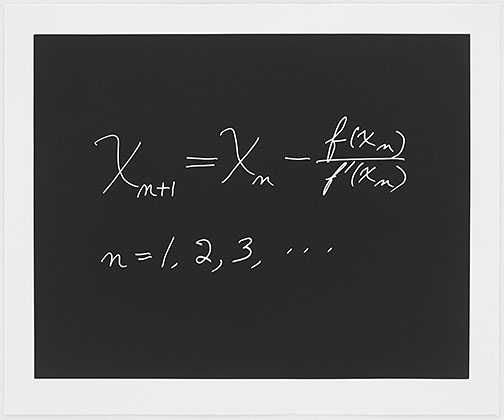Is it Art?
A couple of years ago, my good friend Dan Rockmore sent me by FedEx a remarkable invitation: write on copper plate "what you think is your most significant and elegant equation", for a limited edition of etchings. Even for Dan whom I've known for unorthodox projects, this seemed off the wall. But OK: Yole Zariski, the wife of my PhD advisor Oscar Zariski, had her artist brother cast some of Oscar's results on a necklace that she loved. Maybe the odd symbols that we put together might be viewed as a contemporary form of magic and, even if not understood, with a McLuhan-esque significance. And now, I learned from Dan, the project has expanded and they are seeking everyone's "beautiful mathematical expressions": login here "
Now I've always had a complex attitude towards ART that started with my sister Daphne and brother-in-law (Charles DuBack) being artists and watching them struggle with evolving tastes and fashions and their own muses. Then my oldest son Steve became an artist, my second son Peter became a photographer, I married an artist Jenifer, whose sister Mimo, second son Andrew and his wife Heather are artists and finally Steve married the artist Inka Essenhigh -- you get the picture. Of course we collect a lot of art -- "friends and family" we call it, so I follow prices, galleries, reviews a tiny bit. I'm aware, especially after reading Seven Days in the Art World, of some of the bizarre aspects of the scene. In another direction, I have found striking parallels between the history of art and the history of math going back to 1800 at least (Here's a lecture I gave on this). These are two fields that are not dependent on language and so can express the zeitgeist more directly. In yet another direction, both the Paris school of Jean-Michel Morel and my own research on the statistics of images have led us to synthesize images and we have noticed how naturally some kinds of abstract art emerge.
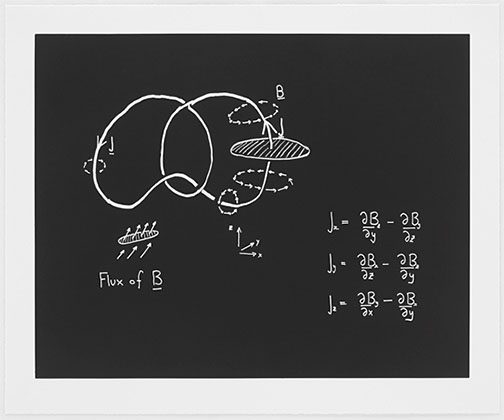
Dan's project had emerged from a serendipitous meeting on a trans-continental flight with an unorthodox publisher, Bob Feldman of Parasol Press, who has created beautiful portfolios of many great artists, so we were in very exalted company. Sol Lewitt is perhaps the best point of reference. Bob had always wondered if math could be made into art and Dan had likewise wondered if art could be made out of math. So this tube full of many types of paper and drawing instruments (no copper plate) arrives in the mail and we spread them out on the dining room table. Thank god that my wife knows art materials and after I play with charcoal a bit, I find I can make believe I am talking to a class and writing on a blackboard. My contribution was a startling identity that arose studying moduli space, most peculiar in having the number 13 appear in it. As I said in the accompanying blurb, the only numbers bigger than 2 that are likely to appear in a math article are usually page numbers. This one has also the merit that it has been used by string theorists.
Now the plot thickens. Together with 9 other mathematicians, physicists and computer scientists, the portfolio was put together using aquatints that inverted the colors, now white on black like chalk on a blackboard. This is apparently an awfully hard process to master, especially with thin lines scratched on the paper. But Harlan and Weaver succeeded and the lot is being sent around the world with the title Concinnitas from art gallery to art gallery: Zurich, Seattle, Portland, Yale. In the sidebar I have put thumbnails of the 10 aquatints for your edification. A panel discussion was arranged at the Yale Art Gallery where I met the full cast of characters. Amazingly, a couple of hundred people showed up to hear the discussion. That's where I heard how challenging the aquatint process was and had the pleasure of meeting Bob Feldman. And we also learned from Yale professor Asher Auel that, like artists with different favorite paints, there are three types of chalk with which mathematicians can make quite different sorts of lines.
Most of the panel discussion, however, centered on the question -- "Is it Art?". In fact, it was reviewed in the Scientific American! I had just seen upstairs in the museum a quite wonderful wall done by Sol Lewitt made from panels with all permutations of two curved arcs, butting up to each other. What he found was that the serendipitous pairings on adjacent panels created a spider web of contours that, for me anyway, "worked" as an entry point for math into art. I was not so sure that any such unanticipated magic emerged from our scrawls, raising them above a status of fetishistic objects for the layman. Still confused about what is art, my wife and I went the next day to stay in NYC with two people in the thick of it -- my son Steve and his wife Inka. Steve told me: "read Tom Wolfe's The Painted Word". And I did. What an eye opener. The whole history of 20th century art began to make sense. If you haven't cracked this slim volume, let me reproduce the quote that sets him off -- from Hilton Kramer in the April 28, 1972 Times (reviewing a show at Yale in fact):
Realism does not lack its partisans, but it does rather conspicuously lack a persuasive theory. And given the nature of our intellectual commerce with works of art, to lack a persuasive theory is to lack something crucial -- the means by which our experience of individual works is joined to our understanding of the values they signify.
He goes on to detail the many theories shilled by art critics that supported all the isms of 20th century art. Now formulas began to seem more plausible as grist for this mill. Minimalism? Conceptual Art? Urban graffiti? Surely there's a place there somewhere for formulas. All it needs is its own unique persuasive theory! Maybe Dan and Bob's projects will have legs.
This post has been translated into Hungarian by Elana Pavlet: CLICK HERE
It has also been translated into German by Laura Fields: CLICK HERE>