Ruminations on cosmology and time
Like many people, I have been riveted for decades by the breathless bulletins from cosmologists describing the latest twist to their model of space and time at the largest possible scale. But recently, I have been looking more closely at these theories and, frankly, do not find them 100% convincing. Maybe it's all true but maybe in 50 years, it will all change. My biggest source of skepticism is its treatment of time: it feels as if in several ways it is trying to undo the vista that special and general relativity opened up for potential models of space-time, that the "standard model" reverts to a very Newtonian perspective on which an extremely simple relativistic model has been foisted. Let me explain.
I. A trip by space ship
I began, a few months ago, wondering how far a space ship, capable of 1G acceleration for decades, could take a human being. I have no idea what its power source might be but 1G means life on the space ship would feel exactly like life on earth if their 'floor' was perpendicular to the acceleration and, when it needed to decelerate, it could just turn around and the astronauts would still be standing normally on the 'floor'. To my astonishment, I found that I could travel to the black hole in the center of the Milky Way galaxy, known as Sagittarius A*, and back, all in less than forty years. Meanwhile, tens of thousands of years will have elapsed on earth when it returns, so forget the greeting committee. That's the magic of relativity. Here are the details.
Let \( \vec x, t \) be space-time coordinates and let \( ds^2 = dt^2 - \|d\vec x\|^2/c^2 \) be its special relativistic metric with s measuring "proper" time along any time-like trajectory (e.g. the subjective time that would be experienced by a human following this trajectory -- I will use "subjective" and "proper" below as synonyms), c the speed of light. The Lorentz group acts transitively on any hyperbola whose asymptotes are light rays (i.e. a curve given by \( c^2(t-A)^2 - (x-B)^2 = R^2 \) ) , hence these are the curves of constant acceleration. Alternatively, the relativistic acceleration of a body whose trajectory is \( x=f(t) \) is readily seen to be \( f'' \big{/} \sqrt{1-(f'/c)^2}\, \) and one can check that this is constant on all such hyperbolas. A hyperbola through the origin and tangent there to the time axis represents the trajectory of an initially stationary space ship with constant acceleration and its trajectory is conveniently expressed as: $$ \vec x = \vec a.\cosh(s/\lambda), \, t = \lambda.\sinh(s/\lambda).$$ Here \( \| \vec a \| =c^2/g, \, \lambda = c/g \) where g is the acceleration of gravity on earth, i.e. 32.174 feet/sec2 and s is proper time in the space ship. If we use years and light-years for units, then \( c = 1 \) and remarkably, \( g \approx 1 \)! More precisely, there are exactly 31,557,600 seconds in a year (the Julian year, as used by the IAU) and about \( 3.104 \times 10^{16} \) feet make a light year, making the acceleration of 1 light-year/year2 about 31.17 feet/sec2. Thus \( g \approx 1.03 \) in light-year and year units.
The latest measurement show that SagA* is about 26,000 light-years away from us. Then if you set \( c=1, g=1.03, s=9.87 \), you find that in less than 10 subjective years, the space ship has gone 13,000 light-years and is half way to the black hole. However, note that t is also 13,000, i.e. on earth 13 millennia have passed. At that point, your speed is \( c.\tanh(10.16) \) or 99.99999985% of the speed of light. In twenty years, you'll be at Sag A* but, of course, prudently not too close. In less than forty years, you are back on an earth where more than 52,000 years have elapsed.
A few caveats: firstly, space-time is not flat, meaning you need some extra power to get out of the sun's gravitational field and you will be accelerated/decelerated by the galaxies gravitation on the way in, resp. way back. I think these are minor. When your own space ship hits its maximum speed midway, everything is normal inside your space ship but outside, stars and interstellar gas are rushing by extremely close to the speed of light. The usual formula shows that their masses increase by the factor \( \left(1-\|d\vec x/dt\|^2/c^2\right)^{-1/2} = \cosh(gs/c) \approx 13000 \). You'll need good shielding. Finally, if you use a photon drive, accelerating by emitting high energy photons and take the mass of the space ship to be the same as that of the space shuttle (2 million kg), my calculations show that the needed energy for this trip is roughly \( 10^{18} \) kilowatt-hours, roughly 10,000 years worth of the total energy being generated today on earth -- seems to need some breakthroughs before we try it. Incidentally, paths that accelerate fast enough, such as \( x=ct+t^{-2} \), get to \( t = \infty \) in finite proper time s, although requiring infinite energy. But see "Black Holes" below for another option. Finally, I want to mention a totally exotic approach to this sort of travel: warp drives. A recent study appeared in arXiv:2102.06824. The idea is to form a traveling bubble by warping space-time so that, within the bubble, both space and time can be scaled differently from their values outside the bubble. In the preprint referenced above, the author claims this to be possible "in principle". For this reference and many invaluable comments and corrections, I want to thank Thomas Buchert whose work will be discussed below.
The key thing for me is that when high relative velocities occur, one should not expect any, even roughly consistent time coordinate to be possible. Fellow humans in the future or members of an alien civilization, are likely to be marching to different drummers. But it is true that measured stellar and galactic velocities are all quite small compared to the speed of light. Individual stars, both in their rotation around the milky way and in their additional so-called "peculiar" motion (this is standard astronomer's lingo for apparently random motion), have speeds with order of magnitude 100 km/sec, <0.1% of c. Even so-called high-velocity stars have speeds <1%, e.g. a record neutron star was found moving at 1500 km/sec. Galaxies have peculiar velocities in that range too. In the Virgo cluster, for example, measured by their red shifts, their recessional velocity varies by plus or minus 1000 km/sec. Our local group of galaxies is believed to have a peculiar velocity of about 600 km/sec. So if other intelligent forms of life exist in our universe, one good sign might be the occasional object moving at extremely large velocities. Science fiction movies have it all wrong: if you want to go far, there is no need to subject yourself to suspended animation, you simply need a huge supply of energy.
II. The Standard Model
This leads us to the standard model of modern cosmology, more precisely, the FLRW or Friedman-Lemaitre-Robertson-Walker model. General relativistic models all rely on a 4-dimensional space-time endowed with a Lorentz metric with signature (1,3). In the local neighborhood of each point, the manifold has coordinates \( (t,\vec x) \) in which the metric is negative definite along t = constant slices and positive definite along the time lines \( \vec x \) = constant (n.b. sometimes the opposite signs are used but I will follow this convention). From this truly vast set of possibilities, the FLRW model comes about by requiring isotropy (invariant under spatial rotations) and spatial homogeniety (invariant under a 3D group of translations), together known as the cosmological principle. This has the drastic effect that the only possible metrics are of the form: $$ ds^2 = dt^2 - \dfrac{a(t)^2}{c^2}.d\Omega^2$$ where \( d\Omega^2 \) is the positive-definite metric on a 3-space with constant sectional curvatures k. It is true that astronomy strongly supports isotropy and the mankind's bad experience with Ptolemaic earth-centered astronomical models supports the idea that the position of the earth is in no way special. But for homogeneity to even make sense, one must choose a distinguished set of spatial translations with respect to which it is homogeneous. And this means taking our local universe and extrapolating it "sideways" into parts of space-time which are totally unobservable from our space-time location. We can only observe things on our past light-cone, the locus of points in space-time from which a light ray might reach us now. In other words, we are trying to make inferences about a 4-dimensional cosmos from data on this 3-dimensional backwards oriented cone. A global space vs. time splitting, as in the FLRW model, is already a huge extrapolation of our limited human observations to a model of the entire universe. I see this model as making a similar error to that of Ptolemy. It would have been more natural to update the idea that we are not in a special point in space by asking that space-time is homogeneous, so we are not in a special space-time location. This is what Einstein initially did. But the red shift and its explanation by an expanding universe (instead of it being a Doppler effect) contradicts this: apparently no reasonable metric for our universe can be invariant under time translation. It is an easy exercise to show that with the above model, light emitted by atoms at time temit and observed by comoving observers of time tobs has its frequency divided by \( a(t_\text{obs})/a(t_\text{emit}) \).
Accepting the validity of the standard model, what does this backwards light-cone look like? One needs to integrate a(t) using Einstein's and Friedman's equations. Fitting the best current data, e.g. the Hubble constant, observational data on galaxies and the small but significant anisotropies of the cosmic microwave background (CMB), the standard model has been made completely specific: in one version anyway, the universe looks uncurved in spatial directions and the stress-energy tensor is made specific with 31.5% energy from massive particles (including "dark matter"), roughly 0.00006% from radiation, and 68.5% from "dark energy" (a non-zero cosmological constant). In recent times, dark energy controls a, for most of the past matter did and at the time of the CMB, radiation was the dominant term. With all these assumptions, Friedman's equations allow one to integrate for a(t).
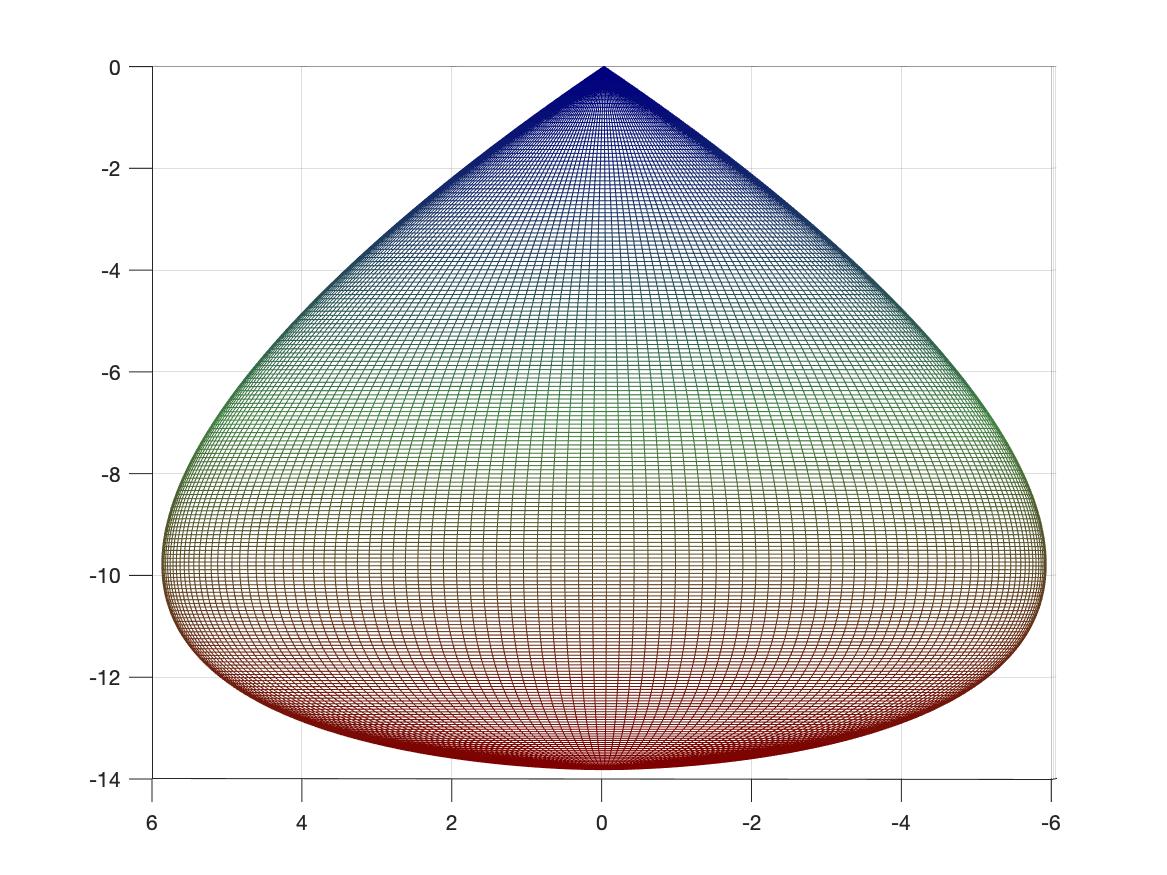
The light-cone starts off, as you look out in space while necessarily also looking back in time, like a cone whose slope is c, one light-year out, one year back. But as you go further out and further back in time, to say around 8 billion years back, to where the Hubble expansion of the universe means space was then smaller, this begins to seriously counteract the expanding sphere of ancient light sources so the cone expands less than linearly. What you're seeing through the telescope when you look 10 billion light-years out or more begins to come from smaller and smaller spheres as measured in the metric at those long past times. At 13.8 billion years back, you hit the cosmic microwave background and see a flash (red shifted to microwave frequencies) and you can see no farther back in time or out in space. Possibly, going beyond photon based astronomy, there is a possibility that gravitational waves may give us data on even earlier states of the universe but this has not been done so far. Remarkably, the diameter of the sphere that produced the CMB that you see on the earth today is then not 13.8 billion light-years across but merely 80 million light-years (according to the standard model). Below is, I believe, an accurate picture of this model of the past light-cone if you make space two-dimensional instead of three. Its surface encompasses everything any telescope can see. We are perched at the cones apex at the top, the vertical axis is time in billions of years, the horizontal axes are distances in billions of light-years. The visible CMB is a circle at the bottom so tiny it is only a point in the figure. The light-cone is colored to suggest (not accurately) the increasing red-shift as you go out in space and back in time.
III. An aside on space-time curvature
Before going further, I want to clarify the meaning of curved space-time. As a mathematician used to Riemannian geometry, I realized after a while that I was confused about the meaning of positive and negative curvature for space-time, especially because the metric is assumed to have signature (+,-,-,-) by some authors and (-,+,+,+) by others. The coefficients of the curvature tensor itself depend on the coordinates and are not so easy to interpret. In Riemannian geometry, what makes geometric sense are (i) the convergence and divergence of nearby geodesics (think great circles on earth converging half way around the world) and (ii) the rate of increase of areas/volumes as their radius increases (think how easy it is to get lost in negative curvature spaces). The simplest coordinate-free scalar curvature variables, ones that depend only the geometry, are the sectional curvatures. These are scalar measures attached to 2-planes in the tangent space by evaluating the Riemann curvature on an orthonormal basis of this plane, or in any basis, dividing by the appropriate 2x2 minor of the metric. I was surprised, however, that the immense tome Gravitation of Misner, Thorpe and Wheeler never mentions these (without an online version, I may have missed this). In general relativity, time-like geodesics are the paths of free falling bodies and their convergence/divergence is highly relevant and can be read off a sectional curvature for a 2-plane containing their two initial trajectories. BUT beware: this is only if you make the coefficient of dt2 positive. If you prefer the convention of making this term negative, with space directions positive (as M-T-W do), you need to reverse the sign to get the right geometric meaning. Sectional curvatures flip signs when the metric flips signs. As for totally spatial 2-planes in general relativity, geodesics here have no physical significance but growth or shrinkage of areas/volumes does. We want spatial sectional curvature to be psoitive (resp. negative) if areas grow less fast (resp. faster) than \( \pi r^2 \). Again, with my convention for the metric, you must flip signs to get the right meaning, but with M-T-W's convention, not so. To be clear, I'll call these the geometric sectional curvatures below. A further issue to be careful about is that the curvature of the time slice t=0 in the induced metric is not the same as the sectional curvatures in its tangent plane: the second fundamental form of the time-slice must be added.
On the other hand, if you consider the Ricci tensor R as a quadratic function on the tangent space, then one way to evaluate R(v. v) on a unit vector v is to take an orthonormal basis including the vector v. Then the sum of the sectional curvatures for all the sections formed from v and one of the others is R(v. v). This is true in the Riemannian case and still holds for indefinite metrics so long as you don't flip signs to make the sectional curvatures geometric.
An important example are the curvatures in the standard model given above. The only variable is the unknown function a(t). The sectional curvatures in the 6 coordinate planes are: $$\begin{array}{cc} \text{2-Plane} & \text{Geometric sectional curvature}\\ \langle t,x \rangle, \langle t,y \rangle, \langle t,z\rangle & -\ddot a \big/ a \\ \langle x,y\rangle, \langle x,z\rangle, \langle y,z\rangle & +\left(\dot a \big/ a \right)^2 \end{array} $$ The signs are confirmed geometrically by considering pairs of geodesics for which x,y,x = cnst, whose distance apart has the factor a(t), as well as geodesics that start in a hyperplane t=cnst but then bend towards the side where a(t) is smaller.
IV. Some alternative models
I am hardly the first person to question the veracity of the standard model. In recent decades, Thomas Buchert at the CNRS Center CRAL in the University of Lyons and David Wiltshire in the University of Canterbury, New Zealand, have been very active in questioning the theory and proposing alternatives. Their basic criticism is that (i) the observed universe is absolutely not homogeneous, (ii) this inhomogeneity is large enough to strongly affect the derivatives of the metric (see Buchert et al, arXiv:0906.0134) and (iii) one cannot simply average out the inhomogeneity because the equations are highly non-linear so that averaging and time evolution do not commute. In fact, it is not even obvious how one ought to average the key tensors like curvature to appropriately summarize their effects. This problem is called "back-reaction", matter affecting space that then affects matter. Buchert has developed extensive machinery for attacking these issues: a recent paper is arXiv:1912.04213v2.
How inhomogeneous is the observed part of our past light-cone? Well, galaxies cluster and these clusters fall into superclusters; the milky way sits inside the "local group" of galaxies (roughly 10 million light years across) which is, in turn, part of the Virgo supercluster (roughly 100 million light years across). But at bigger scales, the superclusters form walls and filaments, e.g. the Sloan Great Wall that is more than a billion light years long. These structures are separated by voids with extremely few galaxies whose size averages about 150 million light-years and which seem to fill about 60-70% of the volume of space today. The whole structure is very fractal-like. There seem to be some even larger structures that one detects from gamma ray bursts and clustered groups of quasars (the radiation from matter furiously accelerated by really big black holes) whose red shift places them at 5-10 billion years old, the equivalent of 5-10 billion years away in today's expanded universe. But this may be the limit because the CMB is very nearly homogeneous and (according to the standard model) is 13.8 billion years in the past.
Wiltshire has worked out the math for a first approximation to an alternative to the standard model that he calls a Timescape Model (see his lecture notes on the arXiv: 1311.3787v2). In this he separates the voids from the wall/filament structures and allows these two types of regions to evolve quite differently. His conclusion is these two did indeed evolve very differently, both in spatial curvature and in their clock (i.e. proper) time. The wall/filament structures in his model maintain near zero curvature while the voids develop strongly negative curvature (I am not sure what convention he is using here). It is the voids that drive the expansion of the universe while gravitational attraction is stabilizing the matter-filled walls/filaments. In his model, by wall/filament clock time, the universe is 14.2 billion years old while clocks in voids would show an age of 17.5 billion years. As soon as you abandon the standard model, there is no reason to assign one number to the age of the universe: it depends on your trajectory from the CMB to the present. Time has no global meaning. Although his model is clearly only a first step, it feels like it reflects the Einsteinian perspective more appropriately in contrast to the simplistic quasi-Newtonian standard model.
V. Black Holes
Black holes have gone from an awkward part of the Schwarzschild model that nobody was sure existed in real space-time to a now ubiquitous and much observed reality in which general relativity gets really wild and wooly. In particular, we are now sure that stars, above a certain size, are fated to collapse, first into neutron stars and then to vanish inside black holes. And we have excellent evidence that almost all galaxies harbor a really huge black hole in their center, like Sag A* in our own galaxy. In fact, one theory for the origin of the "dark matter" that binds galaxies together is that all of it consists of black holes of various sizes. forming a halo around each galaxy. There is a cluster of 73 quasar black holes known as the "Huge LQG", 9 billion light-years away that stretches over billions of light years. To top it off, recently the theory has arisen that our solar system might have a ninth planet that is really a "primordial" black hole (one created at the time of the CMB), merely 5 cm in size but with mass 5x that of whole earth! All this is not surprising since the theoretical results of Hawking and Penrose show that singularities of the black hole type are pretty much inevitable in general relativity.
But the popular conception of black holes as a sort of whirlpool that is sucking people in to their doom is radically wrong, due again to the fact that people cling to the idea that there is one time, valid for all of us. There is a widely accepted model that may well show what is going on inside a black hole but time there is infinitely far in our time's future and, from our perspective, whatever tries to enter the black hole, apparently gets paralyzed (as its local clocks slow to nearly stopping) and then gets redder and redder. The passenger meanwhile has no idea anything special is happening and keeps shining their flashlight to show they are fine as they merrily cross the horizon. But he/she can only send a finite number of photons before crossing the horizon so the signal actually stops as the passenger gets near the horizon. His time has stopped for all intents and purposes while yours moves on. Crazily enough, looking back out the port holes, he/she can still watch what is now long-ago universe with at most moderate red shifts to which they can never go back.
The usual model for a black hole starts with the Schwarzschild model or the more complex rotating Kerr model. Schwarzschild's model exemplifies almost the same time pathologies as the Kerr model, so I'll stick with it. Here it is: $$ ds^2 = \frac{r-r_s}{r}.dt^2 - \frac{r}{r-r_s} dr^2 - r^2(d\theta^2 + \sin^2(\theta)d\phi^2)$$ (we have set c=1, rs is the radius of the black hole horizon and we assume r > rs). If r is large, the metric becomes indistinguishable from flat space-time, so we may identify both its time and space coordinates with our usual (t,x,y,z). In fact, it was devised to model planetary motion with a central mass because its geodesics act as if they are being pulled towards (0,0,0). The fact that the metric apparently explodes when r decreases to rs was a puzzle so the sphere r = rs was called the horizon. But is the metric really going crazy at the horizon? Its Riemann curvature tensor turns out to be "diagonal", i,e. it only has six non-zero entries \( R_{jkjk}, 1 \le j < k \le 4 \) (taking its symmetries into account). The corresponding sectional curvatures are \( -r_s/r^3, \text{ resp. } +r_s/(2r^3) \) for the planes \( \langle t,r \rangle, \langle \theta,\phi \rangle, \text{ resp. } \langle t,\theta \rangle, \langle t,\phi \rangle, \langle r,\theta\rangle \text{ and } \langle r,\phi \rangle \) with singularities only at r=0. Other sectional curvatures are interpolations of these. This is an example of a curvature tensor of the simple "type D" in Petrov's classification (see e.g. the Wikipedia article on this). These are not the "geometric" curvatures, so we can use them to check that the Ricci curvature is zero and most importantly, there is no singularity when r = rs. Note also that the positive curvature in the \( \langle t,\theta \rangle \) plane is geometric and is the main driver of planetary motion. The near periodicity of planetary motion is an immediate consequence of this positive curvature. The negative curvature in the < t,r > plane allows errant bodies to be thrown out of the solar system or to fall into the sun.
Curvature is one thing, but to study the horizon, let's look at how geodesics behave there, taking \( \theta \text{ and } \phi \) to be constant for simplicity (i.e. look at geodesics going directly towards the center (0,0,0)). The simplest ones are the light rays whose trajectories are easy to check: they are given by \( t = -(r + r_s\log(r-r_s)), (r > r_s), \) whose log-term blows up as r decreases to rs, i.e. showing that an infinite amount of "our" clock time is needed for light to reach the black hole horizon. The trajectories of material bodies are given by a messier formula but tell a similar story with the added feature that we can track their proper clock time s as the body approaches to the horizon. Radial geodesics are defined by a diffeomorphism from r going from some large number down to zero and the body's clock time s going from some initial value up to a finite limit, a diffeomorphism that pays no attention to crossing r = rs. On the other hand, t must blow up logarithmically on this path as it does on light rays, hence the fact that when the body crosses the horizon, outside time is infinitely far in the future.
The seeming conundrum of the geodesic continuing in this way is clarified, following Eddington and Finkelstein, by changing the time coordinate in the Schwarzschild metric. Define a new "time" by \( t_{EF} = t + r + \log((r/r_s)-1). \) Using these coordinates, we find that we can enlarge our usual space-time, adding a curious universe inside the black hole whose time is infinitely far in the future: $$ \mathbb{R}(t) \times \left( \mathbb{R}^3(r,\theta,\phi) - \{r \le r_s\} \right) \subset \mathbb{R}(t_{EF}) \times \left( \mathbb{R}^3(r,\theta,\phi)-(0,0,0) \right) $$ for which the new metric has singularities only at r=0: $$ ds^2 = \frac{r-r_s}{r} dt_{EF}^2 - 2 dt_{EF}.dr - r^2(d\theta^2 + \sin^2(\theta)d\phi^2)$$ In these coordinates, space is the same but time has been "corrected" to make the hole's interior continuous with its exterior. Both light rays and material objects moving towards the black hole easily enter this new universe, though, from our standpoint on the outside, they merely slow down, seemingly stuck just outside the hole's horizon. This interior universe is not very friendly because its curvature indeed grows without limit as r goes to zero and all time-like trajectories lead there. A more complete analysis involving an infinitely distant past as well is given either as a modification of Eddington-Finkelstein or the beautiful Kruskal-Szekeres model. My point, though, is that once again we need to forget the idea that time is a universal physical thing. It is rather a thing with distinct existence for each person and there are real possibilities of time-travel into the future, even infinitely far into the future.
I should add one further weirdness about black holes: they pretty much all spin because the matter that created them had non-zero angular momentum. If so, as you approach the horizon, you too must spin (a described by the Kerr metric). In fact, before crossing the horizon, you spin infinitely often. Fortunately, in your local coordinates, you won't get dizzy because it is rotating too. Another twist is that all the matter accumulating at the horizon increases the black hole's mass, hence expands the horizon so stuff really does fall in.
VI. Inaccessible parts of the universe
I want to add a final remark about how strange general relativistic universes can be: it is not only time that goes topsy-turvy in general relativity, but it's space also. It is perfectly possible that there are two parts of one space-time which not only cannot communicate now but where information from one can never reach the other, even in their two futures and vice versa. We are used to the idea that we can explore everything by sending out probes that take pictures and send them back to us. But what can happen is that the pictures coming back are more and more red-shifted, begin to overlap more and more and eventually stop completely at some "border" and never show anything further away. All this without black holes and even in homogeneous universes.
If we accept dark energy, a positive cosmological constant \( \Lambda \), the standard model already illustrates this. In that class of models, the key function a(t), (see equation above in the second section for the formula for the metric) grows exponentially in the presence of dark energy. In fact, apparent recent acceleration of our universe's expansion was the reason why modelers had to include dark energy. As a result, if you wander off even a little bit and wait for while, the universe has seemingly grown so much that you can never get back to your starting place, even if you could go back with speed of light. The reason is that your future light-cone simply fails to meet the space-time trajectory of those who stayed home. Rather than give the formulas here, it's more instructive to look at a very simple 2D case, with one space and one time variable where we can make a helpful picture of this behavior.
This 2D universe is easiest to understand if we start with the one-sheeted hyperboloid \( x^2+y^2-z^2 = R^2 \) with metric \( ds^2 = dz^2 - dx^2 - dy^2 \). Here the vertical coordinate z is like time, while the circles on which
We can apply Brioschi's formula to this expression for the metric and we find that the Gaussian curvature is constant with value \( -1/R^2 \). I find it curious that, although the three constant-curvature spatial surfaces (namely the sphere/the plane/the non-Euclidean plane) are all very well known, this constant-curvature Lorentzian surface is never mentioned. But note that the metric can be given the other sign, making \( \theta \) into time and t into space. Then Brioschi's formula gives \( +1/R^2 \) as the curvature. This is what we discussed in section III: recall that the Jacobi vector fields are determined by lifting indices in the curvature tensor, so in the Lorentz case, predominantly t oriented and predominantly \( \theta \) oriented nearby geodesics behave in opposite fashion, one converging and one diverging. The geometric sectional curvature describe the behavior that is shown here in all cases:
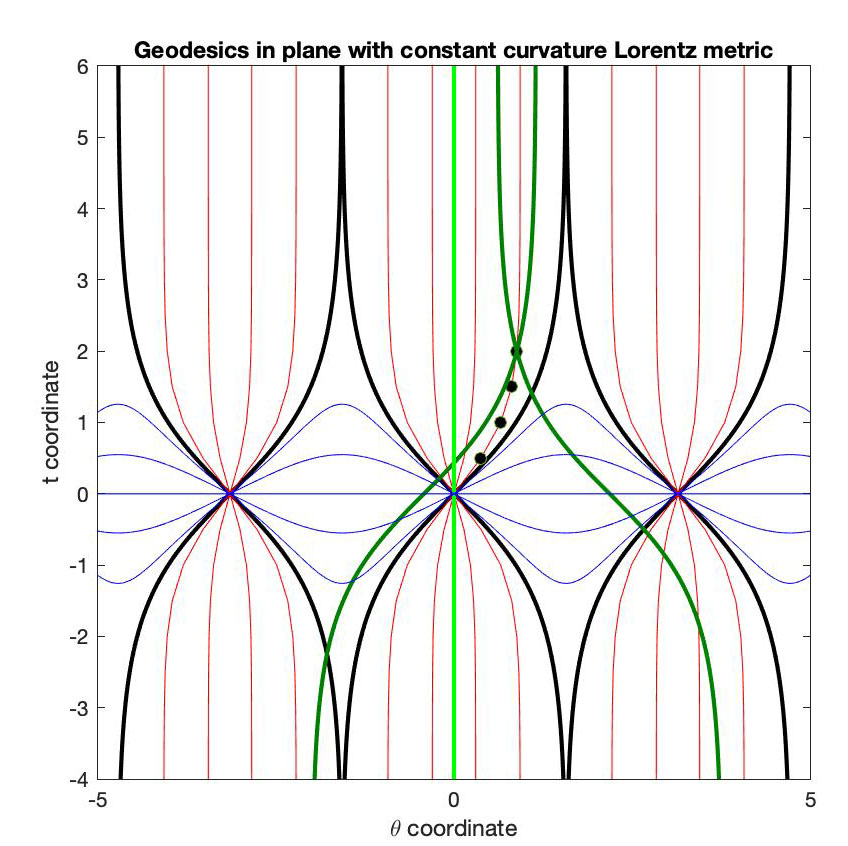
The black lines are the null geodesics ('light rays'), the blue geodesics display positive curvature, having conjugate points when \( \theta \) increases by \( 2\pi \), the red geodesics are actually diverging exponentially, showing negative curvature. It is more natural to regard t as time, \( \theta \) as space. Then the black dots show the path of person in a rocket that takes off at (0,0) and follows a time-like geodesic to the right. At the top dot, he decides to go home but the dark green shows how his future light cone has shrunk as measured by \( a(\theta) \). The dark green lines are new light rays (being horizontal translates of the black ones). The light green line is \( \theta = 0 \), the trajectory of a someone who stays "home". Like someone falling into a black hole, no one in this rocket can ever get "home"! In fact, note that, starting from two points with t = 0, their past and future cones intersect only if their \( \theta \) coordinates differ by less than \( 2\pi \). When this difference is larger, they can never communicate. No matter what their time difference is, neither can ever see into the other's world, let alone travel there. Note too that when they do look at light rays from further away, they are red-shifted: at time t, the frequency of observed light emitted at time 0 by atoms moving on a \( \theta \)=constant path is decreased by the factor cosh(t). Red shifts are, in a sense universal: because of homogeneity, if light is emitted anywhere by atoms moving on a time-like geodesic p1 and you observe it from a comoving time-like geodesic p2 (meaning p2 is perpendicular to the space-like geodesic perpendicular to p1 at the emitter), there will always have a red shift.
Does this have any relevance to 4-dimensional space-time? In fact, following de Sitter, you can use the identical construction starting the one-sheeted hyperboloid in 5-space, giving a space-time metric that is invariant under the orthogonal group SO(1,4). The main difference is that it can't be "unrolled" because topologically it is \( \mathbb{R} \times S^3 \). With a little algebra, it turns out to be the metric: $$ ds^2 = dt^2 - R^2\cosh^2(t/R)(d\Omega^2)$$ Remarkably, this is the unique fully homogenous FLRW metric. Its geometric sectional curvatures for spatial coordinate planes equal \( (\dot{a}/a)^2 = \tanh^2(t) \), hence are always non-negative. Though this varies with t, at every point there will be spatial 2-planes with all curvatures between 0 and 1. For space-time coordinate planes, the geometric sectional curvatures equal \(- \ddot{a}/a \) which is -1 in the above case. For any a(t) growing faster than linearly, more precisely so that \( \int dt/a(t) < \infty \), the same multiple world phenomena occur: two people far enough away from each other can never communicate and if you venture too far off for too long, you can never get home again. Note, however, that all such FLRW worlds, there has to be dark energy to satisfy Einstein's equations.
VII. Final ruminations
From a theory standpoint, there must be huge numbers of possible vacuum or matter filled space-times, with or without dark energy, with complex global structure. Most of these have no tendency to prefer (or even allow) a global splitting of space and time. In this vast array of possibilities, scientists and mathematicians have only explored a handful. A recent book, Exact Solutions of Einstein's Field Equations, another very heavy tome with authors H.Stephani, D.Kramer, M.Maccallum, C.Hoenselaers and E.Herlt, is a pretty exhaustive survey. What it covers, however, are all metrics with some simplifying properties: symmetries, restricted curvature tensors, hypersurfaces in 5-space, metrics gij of special forms. In this pot pourri, however, one truly bizarre example stood out for me and I can't resist describing this. It goes by the name of Taub-NUT metric where NUT is not a suggestion of its weirdness but an abbreviation of the 3 authors Newman, Unti and Tamburino. It starts let's say at time t=0 with space being a constant curvature 3-sphere but with a treacherous second fundamental form in 4D space-time reflecting the Hopf fibration \( S^3 \rightarrow S^2 \). It is only a matter of time before "all hell breaks loose", the fibers of the fibration having lengths going to zero and all time-like geodesics veering wildly away in two directions. Here goes.
If we take the 3-sphere as the unit sphere in complex 2-space z,w, the Hopf map is given by \( (z,w) \mapsto w/z \in \mathbb C \cup \{\infty\} \). If we take coordinates \( \theta,\psi,\phi \) with \( z = e^{t/2}.\sin(\theta/2).e^{i(\psi-\phi)/2} \) and \( w = e^{t/2}.\cos(\theta/2).e^{i(\psi+\phi)/2} \), then \( \theta, \phi \) are the usual angle coordinates on the quotient 2-sphere and \( d\psi + \cos(\theta)d\phi \) is easily checked to be the unit 1-form perpendicular to \( d\theta \text{ and } d\phi \). The idea is to put a metric on the 3-sphere with time varying different weights on the fibers and on the quotient of the Hopf map. We now define the Taub metric on \( (-\ell,+\ell) \times S^3 \)as follows:
$$ \begin{align*}
ds^2 &= \tfrac{\ell^2+t^2}{\ell^2-t^2}dt^2 - \tfrac{4\ell^2(\ell^2-t^2)}{\ell^2+t^2}.(d\psi + \cos(\theta) d\phi)^2\\
& \qquad -{\scriptstyle (\ell^2+t^2)}.(d\theta^2+\sin^2(\theta)d\phi^2)
\end{align*} $$
Remarkably, this choice of coefficients satisfies Einstein's vacuum equations. As t approaches \( \ell \), distance along the Hopf fibers shrinks and space collapses to a 2-sphere. Geodesics, however, do a strange thing: except in symmetric situations, they loop around the Hopf fibers infinitely often while still having finite length! On the left is a picture in the \( t,\psi \) plane, where the blue geodesic (with \( \theta=\phi=0 \) is shown looping around twice (dotted when it comes around):
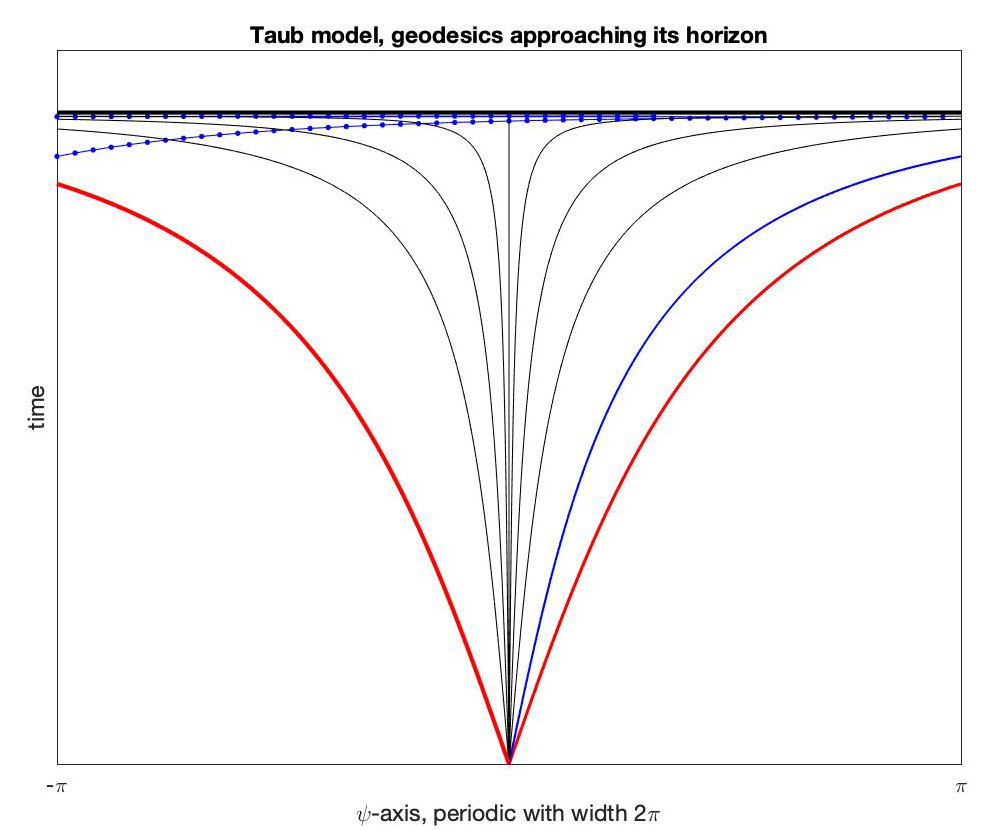
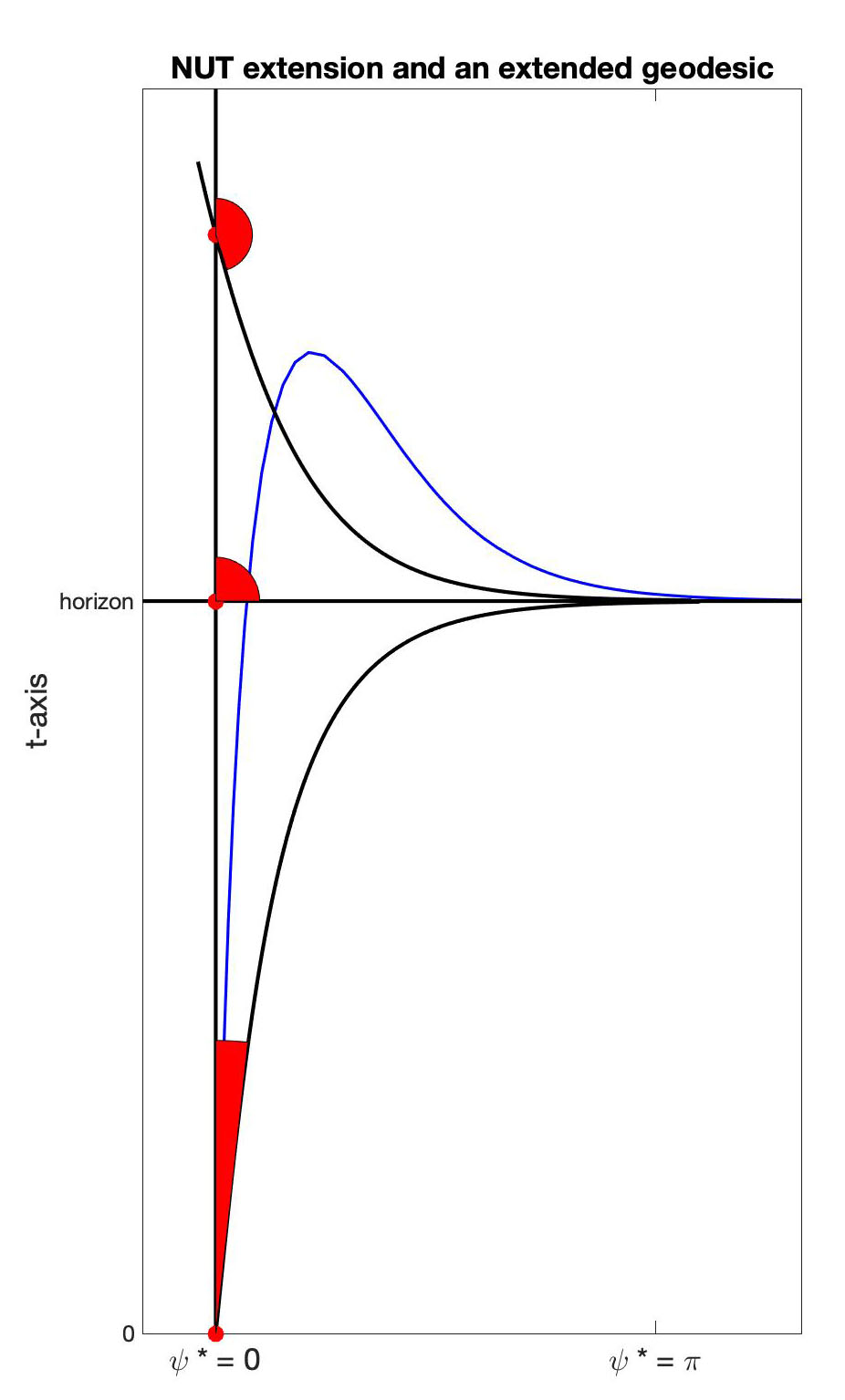
But this isn't the craziest thing about this model. What the NUT authors showed was that, just like the black hole case with the Eddington-Finkelstein substitution, one can change coordinates and then cross the horizon \( t = \ell \) with no problem. Misner called the resulting space a "Counterexample to Almost Anything". Some of its properties are shown on the right. Everything above the horizon are new points infinitely far to the right in the Taub model. The blue geodesic is the same one shown on the left but now crossing the horizon, making an excursion and curving back to the horizon in a striking way. The thick black lines in the figure are all null geodesics, light rays. The horizon itself is a circular null geodesic.The red zones show the directions of future oriented time-like geodesics: space and time get seriously confused as time-like geodesics above the horizon can curve back towards the horizon. To be more careful we need some formulas.
The shift of \( \psi \) giving the NUT-space and the resulting NUT metric are these: $$\begin{align*} \psi^* &= \psi \pm \left(-\tfrac{t}{2\ell} +\tfrac12.\log(\tfrac{\ell + t}{\ell - t})\right)\\ d\psi^* &= d\psi \pm \tfrac{\ell^2+t^2}{2\ell(\ell^2-t^2)}\\ ds^2 &= \pm 4\ell(d\psi^* + \cos(\theta)d\phi).dt - \tfrac{4\ell^2(\ell^2-t^2)}{\ell^2+t^2}.(d\psi^* + \cos(\theta) d\phi)^2\\ & \qquad -{\scriptstyle (\ell^2+t^2)}.(d\theta^2+\sin^2(\theta)d\phi^2) \end{align*}$$ This now a perfectly fine metric on the entire space \( \mathbb{R}(t) \times S^3 \). Moreover, note that ambiguous sign in the metric. There are actually two possible ways to enlarge Taub space beyond the horizon, one extending the geodesics that spin left and the other extending those that spin right. But if you try to patch them both of them onto Taub space, it becomes non-Hausdorff! For example, the vertical geodesic in in the figure crosses every geodesic, whether it's spinning left or right. So in its closure, you get two distinct limits, one in each extension. The blue geodesic shows the fate of all time-like voyagers who cross the horizon: after an excursion into NUT space, they continue to the right, looping around the \( \psi^* \) circle infinitely often while slowly coming back to the horizon. In fact, the picture is even wilder. The whole blue geodesic to infinity has finite length again and, if you take the following coordinate change reveals yet another world: \( \xi = (t-\ell).e^{-(\psi^*+\phi)}, \eta = e^{\psi^*+\phi} \). More carefully, one should first remove the circle \( \theta = \pi \) from the 3-sphere and then unwind it, allowing the angle \( \psi^* \) to be a real number. These ideas were the subject of quite a few papers in the Journal of Mathematical Physics in the 60's and 70's and I have taken this from the 1973 paper by J.G. Miller that appeared there. He showed how the patching continues forever -- see his figure 1, p.490. If I'm not mistaken, this gives an exact and physically possible version of Bill Murray's experiences in the film "Ground Hog Day" where, coming to Punxsutawney to report on the hog, he gets trapped in a world with circular time and ultimately escapes after his circular time spirals sideways long enough for him to find love. Well, except for the saccharine ending, I think the blue geodesic follows the movie closely.
For me, the biggest take-away is the fact that time itself is such a tenuous thing, that hitching your body to light rays or visiting any place where space-time is seriously warped, you break free of the constraints of its normal passage. As Miranda says in the Tempest, the world has such wonders in it. But returning to real life now, any speculation about where cosmology is going must take into account that we are in the midst of an explosion of data from deep space exploration and all sorts of new situations are coming to light. There are indications that galaxy clusters can have coherent motion like galaxies themselves, that huge black holes are not always tucked safely in galaxy cores but can be ejected, reminiscent of Newtonian 3-body solutions in which one body is ejected after a near triple collision. Perhaps the rotations of black holes are not merely a local distortion of space-time and maybe dark matter consists of black holes. Gravitational waves are opening up brand new avenues for probing space-time. However, unless causality itself is violated, our ability to observe and measure the universe will still be limited to observations on or near our past light cone. We can never observe all that much about the interior of our past light-come, unless some sort of cosmic "mirror" is invented or discovered whereby we see the past of our own neighborhood. And we need to wait for eons to pass before we'll see what our cosmic "neighbors" are doing now or before the explorer of Sag A* that I started with returns. I submit that it is likely that we will never to be able to satisfy the human drive to know the "big picture", the beginning and end of "all there is". The confidence of many cosmology popularizers today may wind up sounding as mistaken as the firm conclusions of so many former generations. Two millennia back, Saint Augustine prayed to God to reveal to him the secrets of time. Its subtlety continues to astound.