I enjoy using mathematics to explore and learn about diverse topics in biology and the natural sciences. Much of my research has used topics from applied dynamical systems to study the formation and stability of spatiotemporal patterns. Summaries of recent and ongoing projects are below and more details can be found in my research statement.

Spiral Waves

Spiral waves are common patterns formed in a variety of natural systems. In particular, arrhythmic heart rhythms have been linked to a sustained rotating spiral wave in the electrical activity on the surface of the heart, and spirals are seen in oscillations of chemicals in Belousov-Zhabotinsky reactions. Stable rigidly rotating spiral waves are present in both system, but transitions to complex patterns are common and understanding the bifurcations is important for the applications. I am interested in the stability of spiral waves, and how spectral properties of spirals on bounded domains can provide insight into understanding the instabilities from a mathematical perspective.

Alternans in the Karma Model


Mechanisms Driving Period-Doubling Instabilities


Stationary Line Defect in Rössler Model

In the cardiac setting, an unstable spiral wave can develop into ventricular fibrillation and sudden cardiac arrest (SCA) – the leading natural cause of death in the US. Clinically, the onset of SCA has been linked to the alternans instability, a beat-to-beat alteration in the action potential duration of the spiral bands. Additionally stationary line defects can appear in the Belousov-Zhabotinsky reaction, and lead to a spiral with amplitudes that change abruptly along a radial line. Alternans and line defects are similar mathematically as the bifurcated structures have twice the original temporal period.

We seek to understand the role of spectra in the formation of these period-doubling instabilities, and focus on if and how the domain contributes to the formation of alternans and line defects.


Related work:


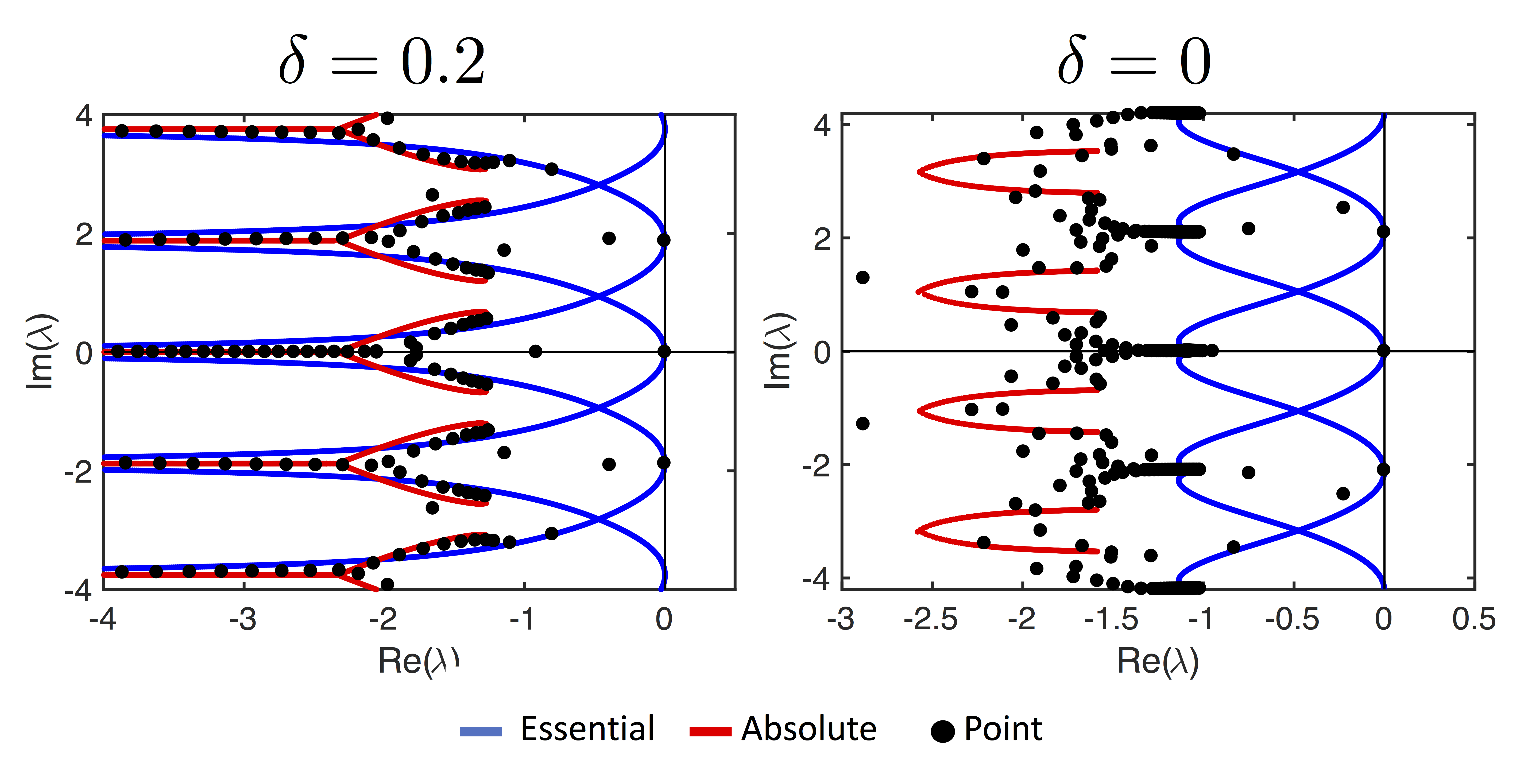
Spectra of Spirals in Reaction-Diffusion Systems with Diffusion-less Species


Reaction-diffusion systems often have one or more diffusion-less species (such as ion-channel models). Numerical results indicate that removing diffusion from a slowly diffusing component dramatically changes the spectra of a 2D spiral; a property that is not observed in 1D. The figure shows the change in the spectra of a spiral in the Barkley model from the slow species slightly diffusing (δ = 0.2) to not diffusing (δ = 0). We are working to analytically and numerically understand why these differences occur and what the implications are.

Related Posters:

Spectra in zero-diffusion limit

A Model for Electrically Excitable Tissue


In collaboration with the Cohen Lab at Harvard University, we developed a PDE model for isradipine Optopatch Spiking Human Embrionic Kidney Cells (iOS-HEK cells), a synthetic excitable tissue. The iOS-HEK cells have simple and well understood ionic channels, but exhibit complex electrical activity similar to cardiac cells. Additionally, the model and experiment highlight how the geometry of the tissue impacts the behavior of propagating electrical waves.

iOS-HEK Cells


iOS-HEK Cells

Article featured on the October 2018 cover of Cell Systems!

Migratory Patterns of Blue Whales


Blue Whale Simulation: Background
indicates prey concentration with yellow high.

Through the 2018 NSF Graduate Research Internship Program, I began working with Dr. Elliott Hazen and Dr. Steven Bograd at the NOAA Environmental Research Division to study the spatiotemporal distribution of blue whales off the California coast. Blue whales are a highly dynamic species, and we developed an agent-based model to investigate how environmental and prey conditions impact the migratory behavior. The model accurately captures the spring-summer northward migration and yearly differences in the spatiotemporal distribution driven by variations in prey abundance. We are now exploring drivers of the fall southward migration.