Research Summary
My research interests
include topological data
analysis with applications
to dynamical systems and biological
phenomena. I am also interested
in the intersection of
topological statistics and
machine learning. In particular, I am interested
in answering questions related
to the robustness of topological
summaries in noisy systems, the
predictive power of topological
statistics in modeling, and the
effectiveness of topological
quantities as input for machine
learning tasks. At present, I work in a range of
applications including zebrafish
stripe development and evolutionary
biology. Below
I give a very brief description
of my research projects. Feel
free to contact me for more
information.
My research is currently
being funded by the National Science Foundation Graduate
Research Fellowship Program.
Any opinions, findings, and conclusions or recommendations
expressed on this website are
my own and do not necessarily
reflect the views of the National Science Foundation.
Current Research Projects
A Topological Analysis of Model Sensitivity and Pattern Formation
My dissertation research is advised by Björn Sandstede and co-advised by Andrew Blumberg. We are interested in applying topological data analysis to study dynamical systems and spatio-temporal pattern formation. Currently I am working on a problem related to classifying model outputs from zebrafish stripe development models. We use topological summaries of the model outputs as input to a classification algorithm. This gives us a way to automatically classify model outputs under various parameter regimes and noise tests. We hope to use this work to better understand these models and the underlying biological mechanisms. Moreover, we use topological methods to study spiral wave patterns and reaction-diffusion models.Hierarchical Clustering of Gene-Level Association Statistics
I work with Samuel Pattillo Smith, Bjorn Sandstede, and Sohini Ramachandran to develop new methods for addressing genomics problems from a machine learning perspective. We recently developed Ward clustering to identify Internal Node branch length outliers using Gene Scores (WINGS), a clustering algorithm for characterizing shared and divergent genetic architecture among multiple phenotypes. WINGS identifies clusters of phenotypes that share a core set of genes enriched for mutations.The above figure shows WINGS applied to PEGASUS gene-level association statistics for 26 phenotypes from the UK Biobank. As shown above, WINGS identifies and ranks clusters of phenotypes with shared genetic architecture. The ranks are determined by the clusters' branch lengths in the corresponding cluster dendrogram (not shown). All clusters on or above the dashed red line are deemed signficant. The significant threshold is determined via WINGS' multi-step branch length thresholding algorithm. Code for WINGS is freely available on Github. For more information, check out our paper.
Topological Estimation of Recombination Rates
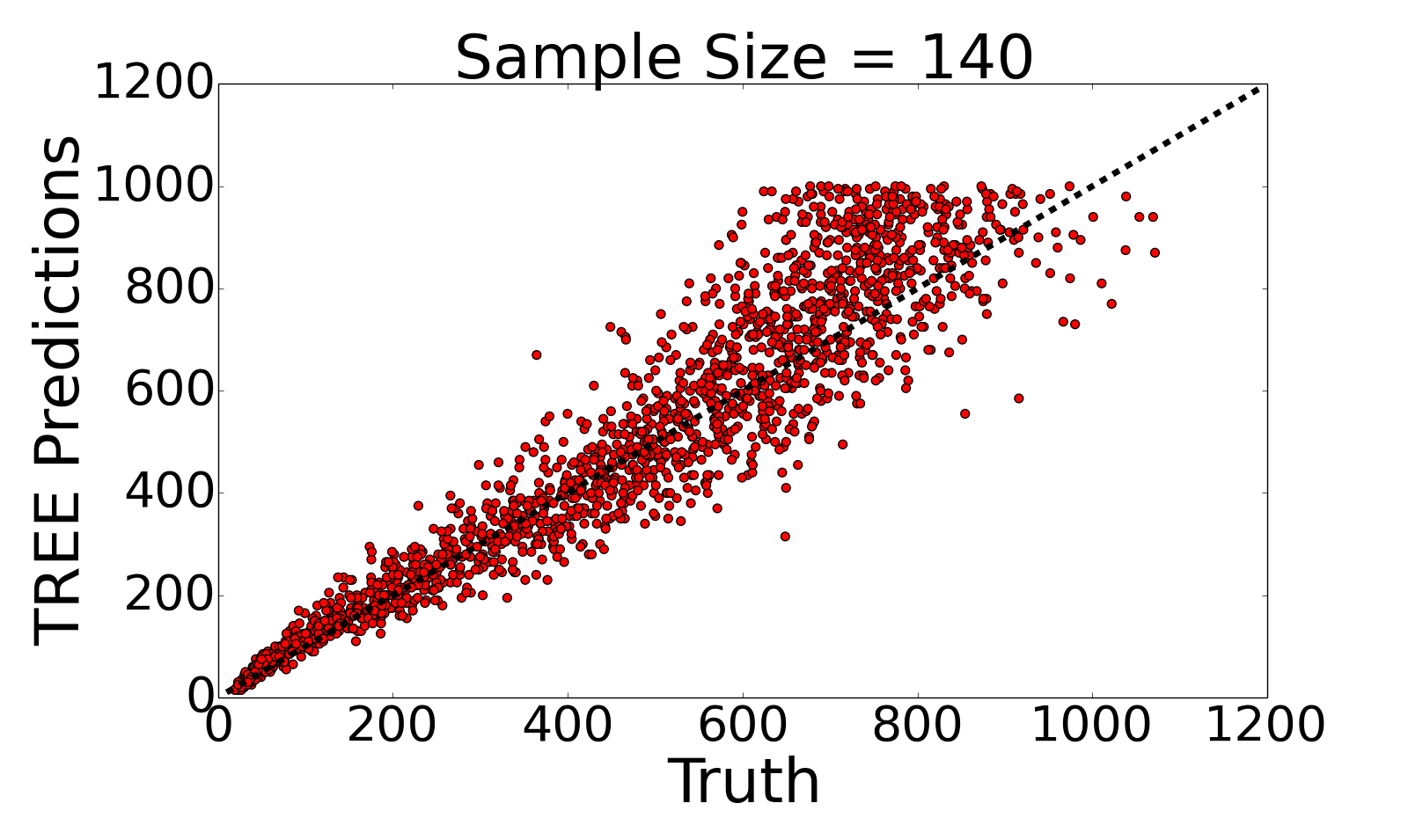
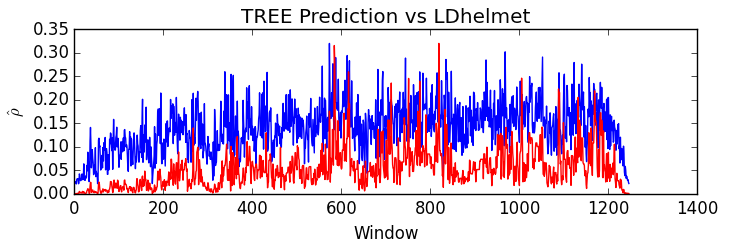
I collaborate with Devon Humphreys and Michael Miyagi under the supervision of Andrew Blumberg on this project. Briefly, we extract topological summary statistics from genomic data and then use techniques from regression analysis to infer hotspots of recombination.We have proposed a novel, efficient estimator for recombination rates based on topological summaries, TREE. Compared to previous TDA methods, TREE more closely approximates the results of commonly used model-based methods and we provide theoretical justifications for the choice of topological summaries.
See below for TREE's predictive performance on simulated data (left) and on an empirical dataset (Drosophila dataset with 22 samples) in comparison to LDhelmet's predictions (right).
Comparing songs without Listening
In the Summer@ICERM 2017 program I began working with Dr. Katherine Kinnaird and undergraduates Erin Bugbee, Claire Savard, and Jonathan Weisskoff on the cover song task. The goal for this project is to develop a flexible and computationally efficient method for completing the cover song task. We use methods inspired from topological data analysis to correctly match songs which are remakes of the same original piece.In this work we propose start-end (SE) diagrams and start(normalized)-length (SNL) diagrams, two novel structure-based representations for sequential music data. Inspired by TDA, these diagrams are equipped with efficiently computable and stable metrics which are then used to address the cover song task. SE and SNL diagrams stem from Aligned Hierarchies (introduced by Katherine M. Kinnaird in this ISMIR paper) but they overcome many of the limitations of Aligned Hierarchies while addressing the cover song with higher accuracy. See below for sample SE and SNL diagrams produced from the Aligned Hierarchies representation of a song.
This work in collaboration with Katherine Kinnarid, Erin Bugbee, and Claire Savard. Congratulations to Claire and Erin for winning the MAA "Outstanding Poster Award" at the 2018 Joint Mathematics Meeting where they presented our work! Our paper, "SE and SnL diagrams: Flexible data structures for MIR" was accepted for publication in the Proceedings of the 19th ISMIR conference.
Research Group
Professor Sandstede's research group participates in weekly meetings each semester where we discuss topics in dynamical systems and related fields. Below is an overview of our meetings along with some of the presentations I have given.| Semester | Main Theme | My Subtopic | Presentation |
|---|---|---|---|
| Fall 2019 | Probability and Statistics | TBA | TBA |
| Spring 2019 | Data-driven modelling and analysis | Discovering equations from data | Here. |
| Fall 2018 | Agent-Based Modeling | Calcium Dynamics | Group Work |
| Spring 2018 | Probability and Statistics | Classification Algorithms | Lecture and Python Demo | Fall 2017 | Dynamics and Statistics | Parallel Computing in Matlab | Interactive demos |
| Spring 2017 | Data Science | Methods of Machine learning | Here. |
| Fall 2016 | Vegetation Patterns | TDA and Diffusion Maps | Here. |