About

This seminar, which operates under the broad aegis of the Data Science Initiative (DSI), will host a variety of speakers whose research lies at the intersection of geometry and topology with data science, biostatistics, engineering, etc. The talks will explore both the mathematical tools developed to address modern data-theoretic challenges as well as discuss recent and ongoing applications. The seminar is aimed at a wide academic audience as part of the DSI's commitment to interdisciplinary research and broad community engagement.

For the 2018 spring semester, the Applied Topology and Geometry Seminar at Brown will be held on Thursdays at 4pm (unless otherwise specified) in the Foxboro Auditorium, Kassar House. This seminar is complimented by the the Data Science Initiative Colloquia.

If you have any questions or are interested in speaking at this seminar please contact Elchanan (Isaac) Solomon (yitzchak_solomon at brown dot edu) or Melissa McGuirl (melissa_mcguirl at brown dot edu).

This seminar is supported by the Data Science Initiative and the NSF TRIPODS grant.

Upcoming Events

This seminar will not run in Fall 2018, check back for updates in Spring 2019!

Past Events

Spring 2018

Date	Speaker	Title and Abstract
May 3	Benjamin Kimia	Similarity Manifold of Shapes and Images Similarity is a key concept in organizing a representation space in computer vision. Two examples are illustrated here, one for organizing the shape space and one for recovering image correspondence. In both examples, it is argued that the topological representation of shapes and images does not require dimensionality reduction per se. Rather, it is important to capture the underlying manifold, especially when millions of exemplars are available. This emphasis requires incremental construction and efficient indexing methods that are suitable for a very large dataset. This talk aims to stimulate a discussion of possible paths forward.
April 26	Carina Curto	Graphs, neural networks, and emergent dynamics in the brain Many networks in the brain display internally-generated patterns of activity -- that is, they exhibit emergent dynamics that are shaped by intrinsic properties of the network rather than inherited from an external input. While a common feature of these networks is an abundance of inhibition, the role of network connectivity in pattern generation remains unclear. In this talk I will introduce Combinatorial Threshold-Linear Networks (CTLNs), which are simple "toy models" of recurrent networks consisting of threshold-linear neurons with effectively inhibitory interactions. The dynamics of CTLNs are controlled solely by the structure of an underlying directed graph. By varying the graph, we observe a rich variety of nonlinear dynamics including: multistability, neuronal sequences, and complex rhythms. These patterns are reminiscent of population activity in cortex, hippocampus, and central pattern generators for locomotion. I will present some new theorems about CTLNs, and explain how they allow us to predict features of the dynamics by examining properties of the underlying graph.
April 5 *This talk will be at 3pm in Barus and Holley 158 *	Lori Ziegelmeier	Persistence Images: A Stable Vector Representation of Persistent Homology Many datasets can be viewed as a noisy sampling of an underlying space, and tools from topological data analysis can characterize this structure for the purpose of knowledge discovery. One such tool is persistent homology, which provides a multiscale description of the homological features within a dataset. A useful representation of this homological information is a persistence diagram (PD). Efforts have been made to map PDs into spaces with additional structure valuable to machine learning tasks. We convert a PD to a finite-dimensional vector representation which we call a persistence image (PI), and prove the stability of this transformation with respect to small perturbations in the inputs. The discriminatory power of PIs is compared against existing methods, showing significant performance gains. We explore the use of PIs with vector-based machine learning tools, such as linear sparse support vector machines, which identify features containing discriminating topological information. Finally, we present novel applications arising from dynamical systems which reveal the discriminatory power of PIs.
March 22 *CANCELLED*	Konstantin Mischaikow	Reduction and Reconstruction of Complex Spatio-Temporal Data It is almost cliche at this point to note that high dimensional data is being collected from experiments or generated through numerical simulation at an unprecedented rate and that this rate will continue rising extremely rapidly for the foreseeable future. Our interest is in data associated with high dimensional nonlinear complex spatiotemporal dynamics. The focus of this talk is on our efforts to use persistent homology both as a dimension reduction technique and a technique for reconstructing structures of the underlying dynamical system. I will present some results associated with dynamics of fluid convection and dense granular media and will try to highlight open questions.
March 15	Andrew Blumberg	Approximating the Gromov-Hausdorff distance Distances between point clouds play an important role in the topological and geometric analysis of data. A theoretically important metric is the Gromov-Hausdorff distance; however, this is not usually feasible to compute. In this talk, I will give an overview of standard approaches to finding tractable distances and then describe some recent work with Villar, Bandeira, and Ward that applies techniques from convex optimization.

Fall 2017

Date	Speaker	Title and Abstract
December 7	Pablo Camara	A topological approach to the identification of elusive cancer genes Developing targeted cancer therapies requires the stratification of cancer patients according to the molecular alterations that are relevant for tumor progression. Commonly used methods for identifying cancer-associated mutations seek signatures of positive selection based on recurrence across large cohorts of patients. However, these strategies have limited power to identify functional variants that occur at low frequencies or in hyper-mutated tumors. Building upon Mapper representations, we have devised a general unsupervised framework for feature selection. In this talk, I introduce the general framework and present its application to the identification of cancer-associated mutated genes. Our goal is to identify new potential therapeutic targets that, because of their low prevalence, have remained elusive to current methods of detection.
November 2	Anthea Monod	Tropical Sufficient Statistics for Persistent Homology with a Parametric Application to Infectious Viral Disease In this paper, we show that an embedding in Euclidean space based on tropical geometry generates stable sufficient statistics for barcodes --- multiscale summaries of topological characteristics that capture the "shape" of data, but have complex structures and are therefore difficult to use in statistical settings. Our sufficiency result allows for the assumption of classical probability distributions on Euclidean representations of barcodes. This in turn makes a variety of parametric statistical inference methods amenable to barcodes, all while maintaining their initial interpretations. In particular, we show that exponential family distributions may be assumed, and that likelihoods for persistent homology may be constructed. We conceptually demonstrate sufficiency and illustrate its utility in persistent homology dimensions 0 and 1 with concrete parametric applications to HIV and avian influenza data.
October 26 ** This talk will be at 4pm in the Foxboro Auditorium **	Attila Gyulassy	Feature Driven Exploration of Images Using Topology Two- and three-dimensional images arise in a multitude of disciplines, from computer simulations to experimental sources such as microscopy. A key step to scientific discovery is extracting semantic information from image data. This talk presents practical application of Morse theory to extract and reason with features intrinsic to images. We will discuss both practical algorithms for computing the Morse-Smale complex as well as real-world applications drawing on imaged and simulated examples from material science, basic energy research, geologic exploration, and neuroscience.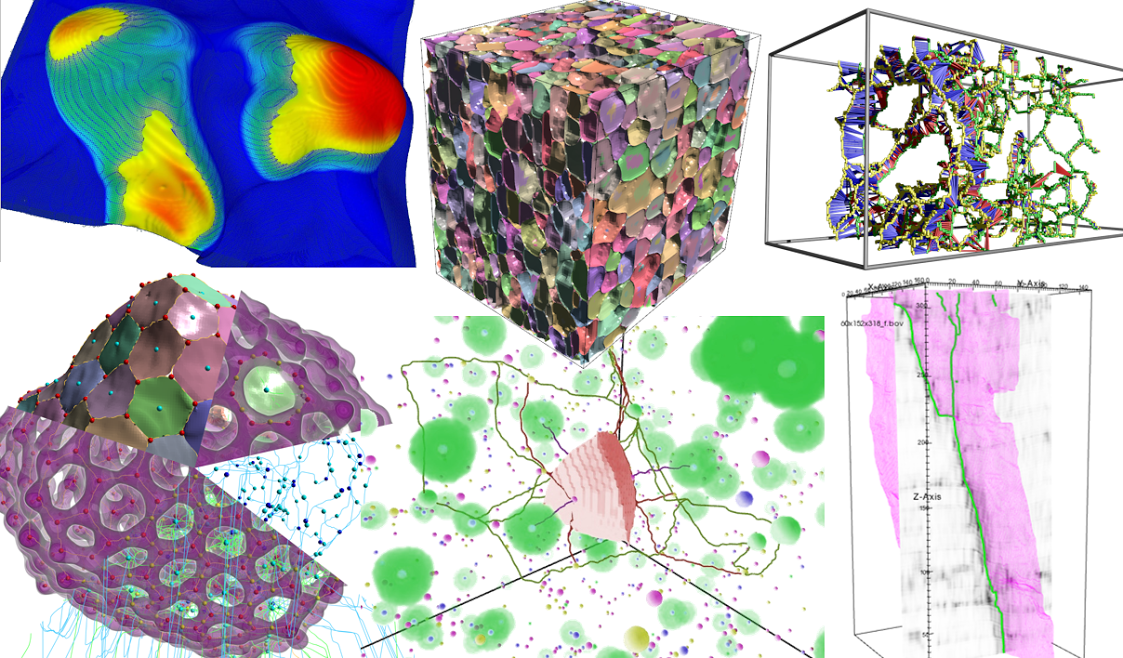
October 19	Lorin Crawford	Functional Data Analysis using a Topological Summary Statistic: the Smooth Euler Characteristic Transform In this talk, we introduce a novel statistic, the smooth Euler characteristic transform (SECT), which is designed to integrate shape information into regression models by representing shapes and surfaces as a collection of curves. Due to its well-defined inner product structure, the SECT can be used in a wider range of functional and nonparametric modeling approaches than other previously proposed topological summary statistics. We illustrate the utility of the SECT in a radiomics context by showing that the topological quantification of tumors, assayed by magnetic resonance imaging (MRI), are better predictors of clinical outcomes in patients with glioblastoma multiforme (GBM). We will close by showing that SECT features alone explain more of the variance in patient survival than gene expression, volumetric features, and morphometric features.
October 5	Elchanan Solomon	A Homology-Based Metric on the Space of Metric Graphs In order to find structure in a large data set it is important to be able to compare data points. For example, if Netflix wants to recommend a movie to you that is popular with similar users, it must first decide what it means for two users to be similar. For data sets consisting of vectors or matrices there are many good ways of making such comparisons. However, a lot of data comes to us in the form of a shape: e.g. a social network graph, an MRI scan, a triangulated 3D model. How can we reasonably and effective compare these shapes? The goal of this talk is to introduce an applied-topology-based approach for comparing graphs that was first considered in a paper of Dey, Shi, and Wang in 2015. This will require a quick introduction to metric geometry and persistent homology for which we will assume no background. Their comparison metric enjoys good theoretical and computational properties, however it is possible for it to conclude that two distinct graphs are distance zero from each other. We conclude the talk with a recent result of Oudot-S. (paper in preparation) that this generically does not happen.
September 21	Justin Curry	The Fiber of the Persistence Map The persistence map is the map that sends a function on a topological space to it's collection of persistence diagrams, which are canonical invariants of filtering a space by sublevel sets and taking homology in each degree. Geometrically, a persistence diagram is simply a configuration of points in the plane. In this talk I will study which configurations of points are possible and what the ramification of this map is for the simplest possible case---functions on the -- --interval. This talk is based on a recent arXiv preprint (arxiv.org/abs/1706.06059) and will require minimal background to understand.

Spring 2017

Date	Speaker	Title and Abstract
April 27	Ellen Gasparovic	A Persistence-Based Summary for Metric Graphs In this talk, we will focus on giving a qualitative description of information that one can capture from metric graphs using a certain topological summary. In particular, we will give a complete characterization of the 1-dimensional persistence diagrams for metric graphs under a particular intrinsic setting. Time-permitting, we will also look at two persistence-based distances that one may define for metric graphs and discuss progress toward establishing their discriminative capacities.
April 20	Sayan Mukherjee	The Geometry of Synchronization Problems and Learning Group Actions We develop a geometric framework that characterizes the synchronization problem --- the problem of consistently registering or aligning a collection of objects. The theory we formulate characterizes the cohomological nature of synchronization based on the classical theory of fibre bundles. We first establish the correspondence between synchronization problems in a topological group G over a connected graph Γ and the moduli space of flat principal G-bundles over Γ, and develop a discrete analogy of the renowned theorem of classifying flat principal bundles with fixed base and structural group using the representation variety. In particular, we show that prescribing an edge potential on a graph is equivalent to specifying an equivalence class of flat principal bundles, of which the triviality of holonomy dictates the synchronizability of the edge potential. We then develop a twisted cohomology theory for associated vector bundles of the flat principal bundle arising from an edge potential, which is a discrete version of the twisted cohomology in differential geometry. This theory realizes the obstruction to synchronizability as a cohomology group of the twisted de Rham cochain complex. We then build a discrete twisted Hodge theory --- a fibre bundle analog of the discrete Hodge theory on graphs --- which geometrically realizes the graph connection Laplacian as a Hodge Laplacian of degree zero. Motivated by our geometric framework, we study the problem of learning group actions --- partitioning a collection of objects based on the local synchronizability of pairwise correspondence relations. A dual interpretation is to learn finitely generated subgroups of an ambient transformation group from noisy observed group elements. A synchronization-based algorithm is also provided, and we demonstrate its efficacy using simulations and real data. joint work with: Tingran Gao and Jacek Brodzki
April 13	Zvi Rosen	From Combinatorial Codes to Realizing Arrangements A combinatorial neural code is a set of 0-1 vectors (codewords) derived from the non-empty non-covered regions of a collection of sets in R^n. Inspired by applications, we study arrangements whose sets are (a) convex, (b) half-spaces, and (c) intervals. Our question: How do topological properties of the arrangement translate into combinatorial properties of the code? We use tools from commutative algebra, topology, and discrete geometry to place some necessary conditions and describe the minimal dimension of a realizing arrangement. Based on joint work with C Curto, E Gross, V Itzkov, J Jeffries, A Kunin, K Morrison, M Omar, A Shiu, N Youngs, and Y Zhang.
April 13	Carl McTague	A New Approach to Euler Calculus I will describe a new approach to Euler calculus—a subject rooted in algebraic geometry which has recently found surprising applications to data analysis. The new approach relies on differential geometry and extends Euler calculus to continuous integrands. It requires a metric but is nevertheless defined within any O-minimal theory. It satisfies a Fubini theorem and extends to a functor. Passing to the “adiabatic limit” recovers the classical Euler calculus. This suggests new applications of differential geometry to data analysis.
April 6	Yitzchak Solomon	Spectral Methods in Computational Geometry Spectral geometry aims to study the geometry of a Riemannian manifold through the eigenvalues and eigenfunctions of various differential operators. The case of the Laplace-Beltrami operator has been the most well-studied, and is related to the heat flow on the manifold. Although one cannot always "hear the shape of the drum", as Weyl conjectured, this spectrum contains a lot of geometric information. Recent work of Memoli and others have shown how to use this spectral data to define a metric on the space of shapes, as well as effectively construct isometries and approximate isometries. In this talk we will review the basics of spectral geometry and survey some of these referenced applications.
March 20 (Monday!!)	Greg Henselman	Combinatorial Homology: A Simplified Approach to Persistence and Computation, via Matroids A basic notion in modern topological data analysis (TDA) is the idea of a persistent homology group. The elements of homological persistence have existed since at least the mid 1980’s, emerging independently in the work of Robins in shape theory, of Edelsbrunner, Kirkpatrick, and Seidel in biogeometry, and of Frosini and Ferri in size theory. Two principle challenges in modern TDA center on questions of modeling and computation: what do persistent homology groups have to say about empirical data, and how can they be computed? A recurring issue in the face of these challenges has been the body of algebraic machinery needed to make the idea of persistent homology precise; this apparatus, while standard in pure mathematics, poses a basic barrier to entry for newcomers to the field of TDA, and an impediment to formal interpretation of elementary topological statistics. In this talk we introduce a new approach to persistent homology which relies on no algebraic structure whatever, but rather some elementary combinatorial properties of linear independence. This simplified framework yields useful insights into the mathematical descriptors commonly associated to homological persistence - barcodes and generators - as well as computation. As an application, we will discuss a new algorithm to compute barcodes and generators, recently implemented in the Eirene library for computational persistence, and its advantages for large and high-dimensional data sets.
March 16	Henry Adams	The theory of Vietoris-Rips complexes Given a metric space X and a distance threshold r > 0, the Vietoris-Rips simplicial complex has as its simplices the finite subsets of X of diameter less than r. A theorem of Jean-Claude Hausmann states that if X is a Riemannian manifold and r is sufficiently small, then the Vietoris-Rips complex is homotopy equivalent to the original manifold. Janko Latschev proves an analogous theorem for sufficiently dense samplings. Little is known about the behavior of Vietoris-Rips complexes for larger values of r, even though these complexes arise naturally in applications of using persistent homology. We describe how as r increases, the Vietoris-Rips complex of the circle obtains the homotopy types of the circle, the 3-sphere, the 5-sphere, the 7-sphere, ..., until finally it is contractible. These homotopy types are related to cyclic and centrally symmetric polytopes and orbitopes. Interestingly, certain Vietoris-Rips complexes of ellipses contain ephemeral summands in their persistent homology modules. We argue that infinite Vietoris-Rips complexes should be equipped with a different topology: an optimal transport or Wasserstein metric thickening the metric on X. With this new metric, we describe the first change in homotopy type (as r increases) of Vietoris-Rips complexes of higher-dimensional spheres. Joint work with Michal Adamaszek, Florian Frick, and Samadwara Reddy.
March 9	Liz Munch	The Convergence of Mapper Mapper, a powerful tool for topological data analysis, gives a summary of the structure of data with respect to a filter function and a cover of the function range. Assuming that this data comes from a true, underlying (but possibly not accessible) topological space, a related construction, the Reeb graph, can be thought of as the ground truth and Mapper, its approximation. In particular, working with a better data sample and/or a more refined cover intuitively results in a Mapper graph which is more similar to the Reeb graph. In this talk, we will discuss a method for defining a distance on these objects via the interleaving distance idea from persistent homology. We can look at various ways to rigorously quantify the idea that Mapper converges to the Reeb graph, as well as ideas for approximation methods of the distance itself.
March 2	Elina Robeva	Orthogonal Tensor Decomposition A symmetric tensor is orthogonally decomposable if it can be written as a linear combination of tensor powers of n orthonormal vectors. Such tensors are interesting because their decomposition can be found efficiently. We study their spectral properties and give a formula for all of their eigenvectors. We also give equations defining all real symmetric orthogonally decomposable tensors. Analogously, we study nonsymmetric orthogonally decomposable tensors, describing their singular vector tuples and giving polynomial equations that define them. In an attempt to extend the definition to a larger set of tensors, we define tight-frame decomposable tensors and study their properties.
February 23	Don Sheehy	What Can Persistent Homology Tell Us About Frechet Distance? We show how to relate the Frechet distance between curves to the bottleneck distance between the persistence barcodes of distance functions induced by the curves. Specifically, we show how computing some persistence-based signatures can yield lower bounds on the Frechet distance. This approach is very general and applies to surfaces and other images of topological spaces into metric spaces.
February 23	Rachel Levanger	Studying fluid dynamics with persistent homology Problems in fluid dynamics are notoriously challenging. While models exhibiting a flow trajectory approaching some fixed state are now relatively well understood, systems that are driven far from equilibrium thwart the efforts of many classical analytical methods. Furthermore, simulations are often performed using periodic boundary conditions, introducing symmetries in the system that must be quotiented out in order to study the underlying dynamics, a formidable task when dealing with data lying in such a high-dimensional space (the space of ideal solutions of a fluid flow is infinite-dimensional, and even a 400x400 pixel image approximation lives in a 160,000 dimensional space!). In this talk, we will show how persistent homology addresses many of these problems simultaneously, using it as a tool for dimension reduction, shape detection, data exploration, and pattern recognition in a suite of examples: Kolmogorov and Rayleigh-Benard convection flows on a two-dimensional domain, and combustion simulations on a three-dimensional domain.
February 16	Ann Sizemore	Cliques and Cavities in the Human Connectome Encoding the axon bundles between brain regions as a complex network has provided novel insights into brain function and disease. Standard network tools describe local or aggregate global phenomena, however many neural functions occur at the mesoscale, involving complex patterns of interactions between multiple brain regions. Here we employ persistent homology to illuminate essential cycles within the structural brain network which may allow for distributed computations. We present long-lived cycles in multiple dimensions, and demonstrate the non-random nature of these persistent features across eight healthy individuals. Finally we propose implications of these persistent cycles for cognitive function and highlight the potential of this topological view of the brain network.
February 9		Brown University is closed because of a snowstorm.
February 2	David Damiano	A Topological Analysis of SPECT Images of Murine Tumors In this talk we employ computational topology methods to quantify heterogeneous uptake behavior across time series of single-photon emission computed tomography (SPECT) images of murine tumors. This behavior cannot be captured by standard aggregate measures such as per cent injected dose per gram or tumor-to-heart ratio. In particular, we utilize zeroth order persistence diagrams as well as the novel concept of childhood diagrams. Statistical methods are applied to time series persistence and childhood diagrams to detect heterogeneity of uptake within and across study groups in two studies. This behavior is explained in terms of the underlying biological mechanisms.

Fall 2016

Date	Speaker	Title and Abstract
December, January	No seminar.	Happy Holidays!
December 1	Michael Lesnick	An Introduction to Multidimensional Persistent Homology In topological data analysis, we often study data by associating to the data a filtered topological space, whose structure we can then examine using persistent homology. However, in many settings, a single filtered space is not a rich enough invariant to encode the interesting structure of our data. This motivates the study of multidimensional persistence, which associates to the data a topological space simultaneously equipped with two or more filtrations. The homological invariants of these ``multifiltered spaces," while much richer than their 1-D counterparts, are also far more complicated. As such, adapting the usual 1-D persistent homology methodology for data analysis to the multi-D setting requires some some new ideas. In this talk, I'll introduce multi-D persistent homology and discuss some recent progress on this topic.
November 24	No seminar this week	Happy Thanksgiving!
November 17	Vladimir Itskov	Convex codes, Dowker complex, and detecting non-linear matrix factorizations. Many neural systems generate neural activity that can be characterized mathematically as convex codes. A convex code is a subset of the power set $2^{[n]}$ that arises from intersection patterns of convex sets in a Euclidean space. These codes retain topological features of the underlying space of stimuli. Not all codes are convex. What combinatorial properties of a code determine its convexity and what determines its embedding dimension is only partially understood. I will begin by reviewing our recent results on convex codes and the special case of hyperplane codes. I will then explain how hyperplane codes are related to the problem of detecting a matrix factorization, hidden by a non-linearity. I will also present some computational results and end by describing an approach for detection of convexity and dimension bounds of a noisy neural code.
November 10	Steve Oudot	A theoretical framework for the analysis of Mapper Mapper is among the most widely used tools from Topological Data Analysis in the applied sciences and industry. Its output takes the form of a graph whose vertices represent homogeneous subpopulations of the input data. Its main asset for exploratory data analysis lies in its ability to highlight patterns that other methods fail to detect in the data. However, the inherent instability of its output makes it a rather unreliable tool in practice. In this talk I will present some recent contributions to the study of the structural properties of the Mapper graphs. Drawing connections to Reeb graphs and extended persistence theory, I will introduce descriptors for the Mapper graphs, which turn out to be both stable and locally complete. These descriptors can be exploited in the development of a statistical framework to assess the stability of the output of Mapper and to select its input parameters automatically.
November 3	Yuliy Baryshnikov	Euler Characteristics of Exotic Configuration Spaces I will describe generating functions for Euler characteristics of multicolored versions of configuration spaces (generalizing a result by S. Gal) and will explain how and where they can be applied.
October 27	Chad Giusti	What else can persistent homology see? The usual framework for TDA takes as its starting point that a data set is sampled (noisily) from a manifold embedded in a high dimensional space, and provides a reconstruction of topological features of that manifold. However, the underlying algebraic topology can be applied to data in a much broader sense, carries richer information about the system than just the barcodes, and can be fine-tuned so it sees only features of the data we want it to see. I will discuss this perspective broadly, and then focus on few particular approaches with applications to neuroscience.
October 20	Rade Zivaljevic	Algebraic topology and cooperative games In cooperative games `players' create coalitions in order to achieve some common goal (voting games, profit games, `simple games' of von Neumann and Morgenstern, etc.). We study and compare the simplicial complexes arising in cooperative game theory (threshold complexes, simple games) with the complexes arising as obstructors for embedding (mapping) spaces into higher dimensional euclidean spaces without double (multiple) points (Kuratowski graphs, Tverberg-Van Kampen-Flores obstructions, r-unavoidable complexes (Gromov-Blagojevic-Frick-Zigler reduction), etc.).
October 13	Anthea Monod	A Case for Topology and Data In this talk, I will discuss the relevance of topology in statistics and probability theory. I will give an overview of research topics stemming from applied and random topology, a relatively new field resulting from the application of point-set and algebraic topological methods to data that arise from random processes. The use of topological methods to analyze data is particularly applicable to information technology and networks (e.g. analyzing internet traffic and communications systems), physics (e.g. analyzing cosmological data), biology (e.g. brain imaging and studying gene regulation), and engineering (e.g. studying coordinated robotics). From the perspective of statistics, such methods are applicable to data mining and image processing. I will outline the methodology of topological data analysis, and discuss recent results on the algebraic topology of random fields and complexes, which are important settings in statistics. I will then present some problems that are currently being studied. In particular, I will underline some contributions of applied topology to resolving statistical problems, and how statistical methodology can contribute to resolving applied topological problems.