
% matlab
>> a = [ 1 2; 2 1 ]
a =
1 2
2 1
>> a*a
ans =
5 4
4 5
>> quit
16 flops.
%
In this example you started Matlab by (you guessed it) typing matlab. Then you defined matrix a and computed its square ("a times a"). Finally (having done enough work for one day) you quit Matlab.
The tutorial below gives more examples of how to use Matlab. For best results, work them out using a computer: learn by doing!
1 2
3 4
and store it in a variable a, do this: >> a = [ 1 2; 3 4 ]
Do this now: define the matrix a. Do the same with the examples below: work out each of them with matlab. Learn by doing!
To redisplay the matrix, just type its name:>> a
Once you know how to enter and display matrices, it is easy to compute with them. First we will square the matrix a :
>> a * a
Wasn't that easy? Now we'll try something a little harder. First we define a matrix b:
>> b = [ 1 2; 0 1 ]Then we compute the product ab:
>> a*b
Finally, we compute the product in the other order:
>> b*a
Notice that the two products are different: matrix multiplication is noncommmutative.
Of course, we can also add matrices:
>> a + b
Now let's store the result of this addition so that we can use it later:
>> s = a + bMatrices can sometimes be inverted:
>> inv(s)
To check that this is correct, we compute the product of s and its inverse:
>> s * inv(s)
The result is the unit, or identity matrix. We can also write the computation as
>> s/s
We can also write
>> s\swhich is the same as
>> inv(s) * s
To see that these operations, left and right division, are really different, we do the following:
>> a/b
>> a\b
Not all matrices can be inverted, or used as the denominator in matrix division:
>> c = [ 1 1; 1 1 ]
>> inv(c);
A matrix can be inverted if and only if its determinant is nonzero:
>> det(a)
>> det(c)
ax + by = p
cx + dy = q
We can write this more compactly as AX = Bwhere the coefficient matrix A is
a b
c d
the vector of unknowns is x
y
and the vector on the right-hand side is p
q
If A is invertible, X = (1/A)B, or, using Matlab notation, X = A\B. Lets try this out by solving ax = b with a as before and b = [ 1; 0 ]. Note that b is a column vector.
>> b = [ 1; 0 ]
>> a\b

Finally, we will do a little piece of programming. Let a be the matrix
0.8 0.1
0.2 0.9
and let x be the column vector 1
0
We regard x as representing (for example) the population state of an island. The first entry (1) gives the fraction of the population in the west half of the island, the second entry (0) give the fraction in the east half. The state of the population T units of time later is given by the rule y = ax. This expresses the fact that an individual in the west half stays put with probability 0.8 and moves east with probability 0.2 (note 0.8 + 0.2 = 1), and the fact that in individual in the east stays put with probability 0.9 and moves west with probability 0.1. Thus, successive population states can be predicted/computed by repeated matrix multiplication. This can be done by the following Matlab program:
>> a = [ 0.8 0.1; 0.2 0.9 ]
>> x = [ 1; 0 ]
>> for i = 1:20, x = a*x, end
What do you notice? Is there an explanation? Is there a lesson to be learned?
Remark: you have just learned to write a kind of loop, a so-called for loop. This is an easy way to command the machine, in just a few words, to do much repetitive work.
To make a graph of y = sin(t) on the interval t = 0 to t = 10 we do the following:
>> t = 0:.3:10; >> y = sin(t); >> plot(t,y)
Here is the result: 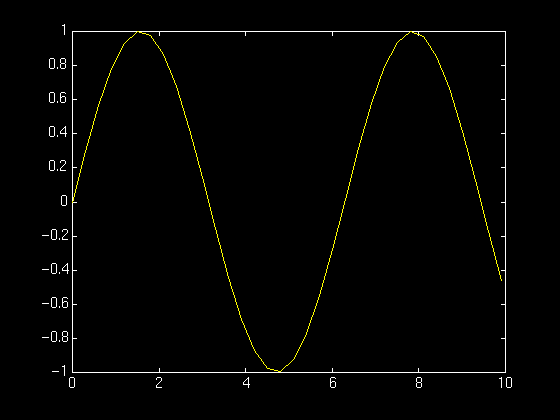
The command t = 0:.3:10; defines a vector with components ranging from 0 to 10 in steps of 0.3. The y = sin(t); defines a vector whose components are sin(0), sin(0.3), sin(0.6), etc. Finally, plot(t,y) use the vector of t and y values to construct the graph.
Here is how we graph the fuction z(x,y) = x exp( - x^2 - y^2):
>> [x,y] = meshdom(-2:.2:2, -2:.2:2); >> z = x .* exp(-x.^2 - y.^2); >> mesh(z)
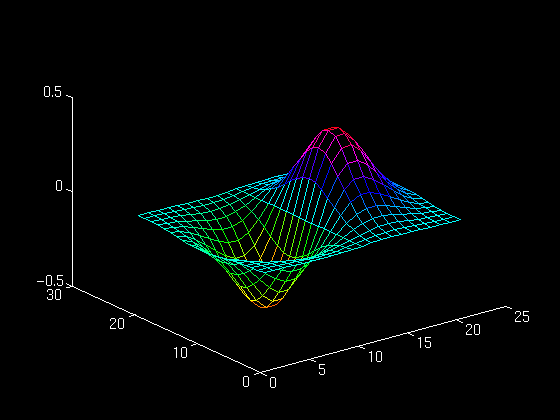
The first command creates a matrix whose entries are the points of a grid in the square -2 <= x <= 2, -2 <= y <= 2. The small squares which make up the grid are 0.2 units wide and 0.2 unit tall. The second command creates a matrix whose entries are the values of the function z(x,y) at the grid points. The third command uses this information to construct the graph.
