Developing algorithms for parallel scientific computing.
Developing algorithms for parallel scientific computing.
My primary area of interest is developing numerical algorithms, visualization methods and
parallel software for multi-scale simulations in fluid
mechanics. Numerical program I'm working with is NektarG - high-order spectral/hp element ultraparallel Navier-Stokes solver.
The solver is build of 4 major modules: Nektar-3D, Nektar-1D, DPD-LAMMPS and MCI (multilevel communicating interface).
The code allows to perform high resolution simulations in 1D and 3D complex arterial networks, and also to perform coupled continuum-atomistic simulations
(under development).
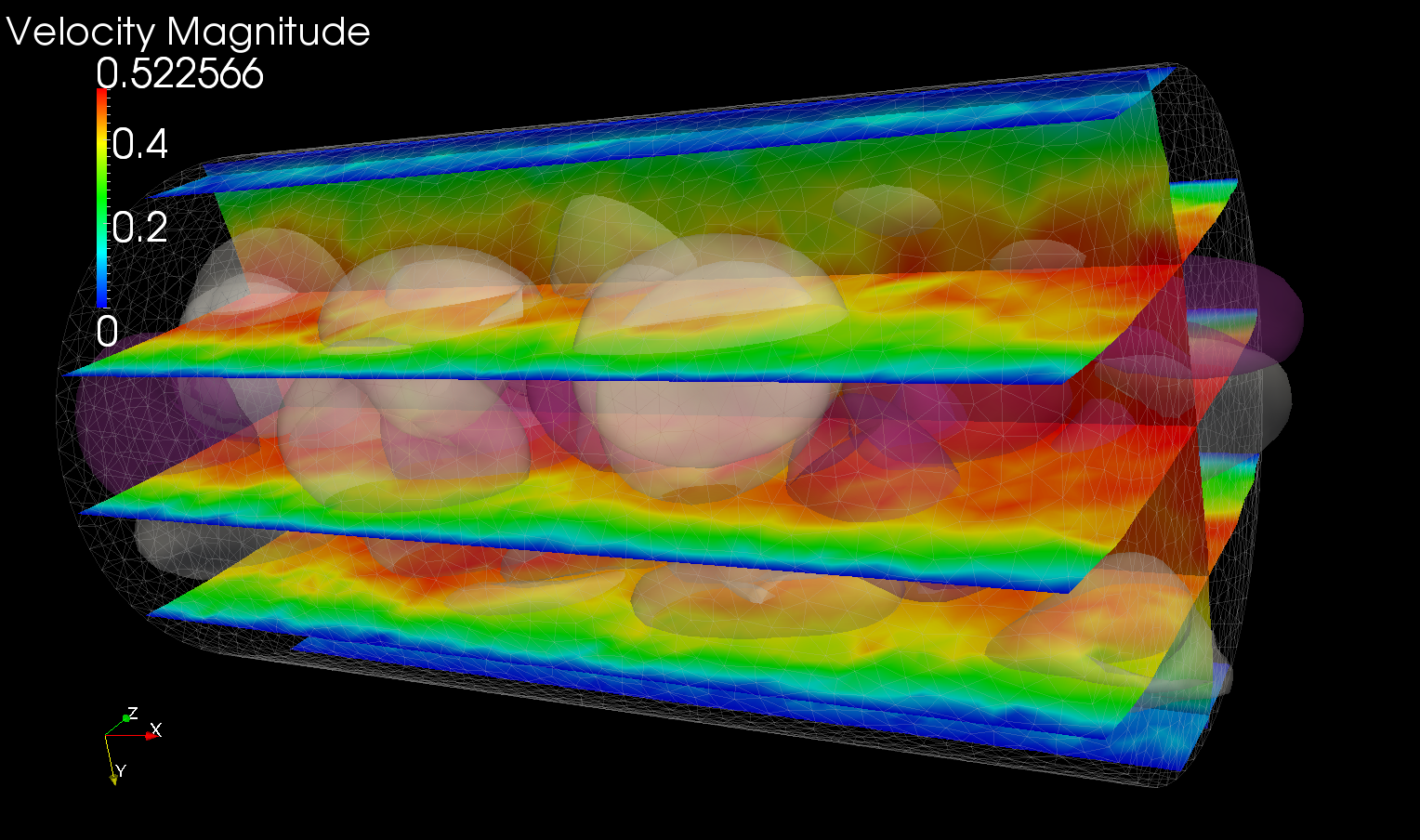
The largest simulation I have performed to solve a "real-life" flow problem
was a multiscale 3D unsteady flow simulation in a domain of brain arteries.
The contunuum solver Nektar has been coupled to the atomistic solver LAMMPS,
the solvers exchange data to impose interface conditions.
The continum domain was discretized into Millions spectral elements,
with about 10 Billions of degrees of freedom.
About 10 Billions of DPD particles were required by the atomistic solver.
This simulation was performed on BlueGene/P of ANL using 72 Racks (294,912 cores);
and also on CRAY XT5 using 190,740 cores.
On the multi-scale front i develop methodology (in collaboration with ANL viz. team: Joseph Insley and Michael Papka) for multiscale viz. Bellow are just a few snapshots (and linked to these snapshots movies) of the multiscale viz. The model of red blood cells employed for multiscale simulations was developed by Dr. D. Fedosov.
For additional visualization please visit this web page.
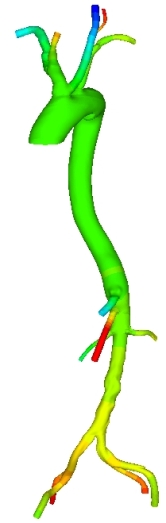
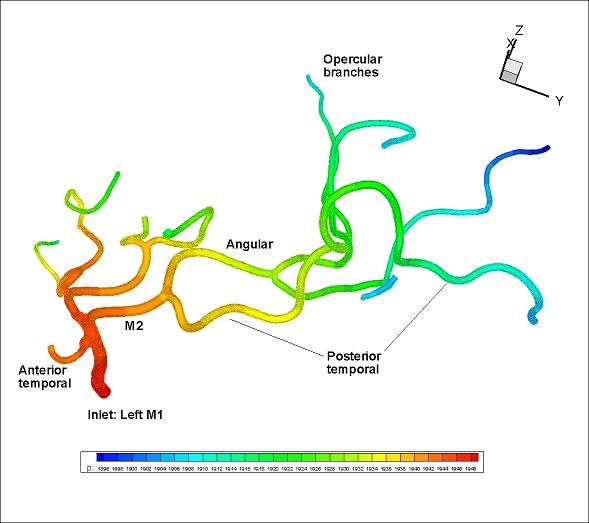
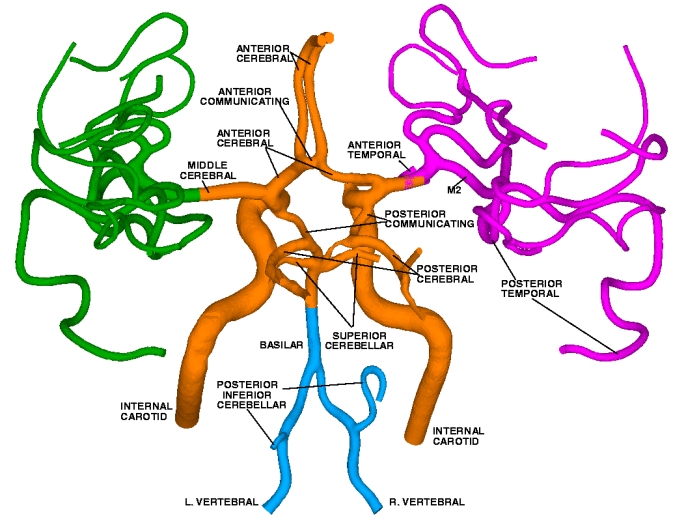
In the left picture we see the reconstructed from CT images model of Aorta with major branches. On the next picture we see the reconstructed model of 20 cranial arteries. Colors depict the pressure distribution on arterial wall. Computational domain of Aorta was subdivided into 325,785 Tetrahedral spectral elements. Numerical solution was obtained with sixth order polynomial approximation (P = 6). Computational domain for cranial arteries included 111,000 Tetrahedral spectral elements, solution was obtained with fourth order polynomial approximation (P = 4). On the right: reconstructed from CTA and MRI images cranial arterial system, the model has 65 arteries, the spectral/hp element discretization of this model leads to computational domain of 470,000 tetrahedral elements where flow equations with over 1E9 degrees of fredom (with P = 6) are solved. Click here to see the 3D geometrical model (AVI movie, 21MB).
 Direct Numerical Simulation of intermittent laminar-turbulent arterial flow.
Direct Numerical Simulation of intermittent laminar-turbulent arterial flow.
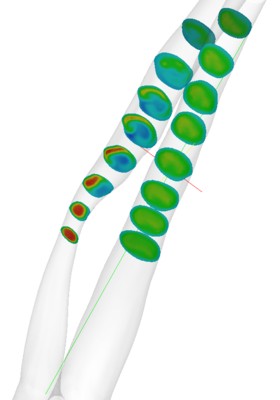
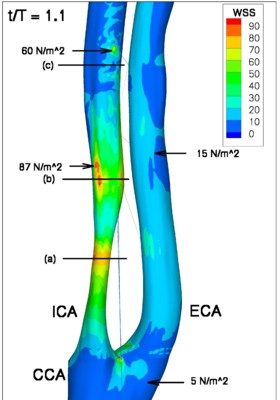
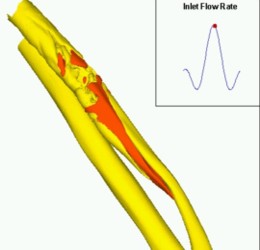
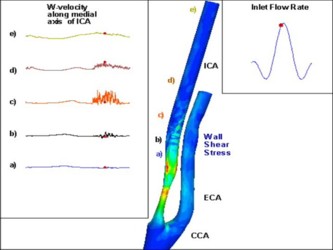
High-resolution three-dimensional simulations (involving 100 million degrees of freedom) were employed to study transient turbulent flow
in a carotid arterial bifurcation with a stenosed internal carotid artery (ICA). The geometrical model was reconstructed from MRI images,
and in vivo velocity measurements were incorporated in the simulations to provide inlet and outlet boundary conditions.
Due to the high degree of the ICA occlusion, variable flow rate and
geometric complexity
a transitional and intermittent flow between laminar and turbulent states was established.
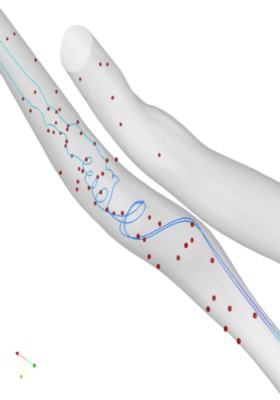
Time- and space-window proper orthogonal decomposition (POD) was applied to quantify the
different flow regimes in the occluded artery (for more detailes please see
publication).
 |
 |
 |
|---|---|---|
| Jet formation | Swirling flow | Wall Shear Stress |
|
|
|
|---|---|---|
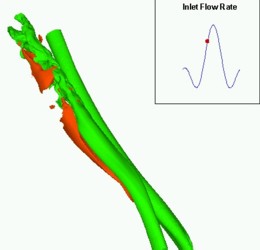
| Turbulent flow. Iso-surfaces of w-component of velocity. |
Turbulent flow. Iso-surfaces of w-component of velocity. |
Turbulent flow. Wall Shear Stress |
 Developing numerical program for reconstruction of arterial wall geometry from CT images.
Developing numerical program for reconstruction of arterial wall geometry from CT images.
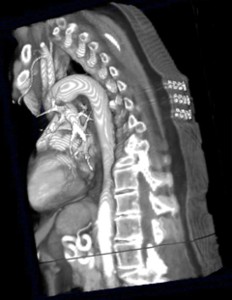
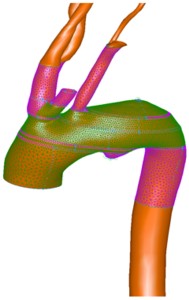
I design and implement numerical software, named "gOREK", for reconstruction of arterial wall geometry. Using Matlab i design
Graphic User Interface to facilitate the process of arterial wall detection.
Due to complexity of arterial network and sometimes poor quality of medical images the reconstructed models have
"missing" regions. Data in this regions can be recovered using Proper Orthogonal Decomposition
and polynomial interpolation techniques.
 |
 |
|---|---|
| 3D CT image | Reconstruction and meshing of aortic arc |