Pythagoras's rule
The earliest extant documents that show knowledge of the rule relating the lengths of the three sides of a right triangle, that is traditionally named after Pythagoras, are Babylonian tablets dating from the centuries around Hammurabi's time, c. 1800 BCE. I am calling it a rule, not a theorem, following Jens Høyrup's suggestion, because it appears as a rule for connecting these lengths, not a theorem, in most of its early history. In any case, we don't know if Pythagoras proved it or not. After the Babylonians it next appears in extant records in Indian Vedic altar construction manuals, composed and transmitted orally as early as 800 BCE. Due to the wholesale destruction of documents in China in the Qin dynasty (221-206 BCE), the earliest records we have for the rule from China date from the second century BCE. This is a sparse set of sources indeed. But because this rule may be described in math-talk as the first "non-trivial" mathematical theorem to be discovered, there has been extensive debate about when and where it was first found, whether it was discovered independently in several places and how it was found. All this work belongs to what André Weil called "protohistory", an attempt to be scholarly when surviving documents are not only sparse but also possibly unrepresentative of a tradition, and totally absent from other cultures. The full history of Pythagoras's rule is a perfect example of a problem on which one can only speculate. But that's what I want to do in this blog. However, all is not speculation and, for great help in all that a real scholar of the History of Math might study, I want to thank Jens Høyrup for all his help.
How should one view such speculation?. My view of history in general, not just protohistory, is that it is always an exercise in Bayesian inference. We never have full knowledge of any past part of space-time. Even in our own lifetimes, we rely on faulty and selective memories in reconstructing events. Scholars have the illusion when they are relying only on primary sources that they not making significant inferences but I believe they are mistaken. Of course primary sources are infinitely better than secondary ones, but everyone has built up their personal prior on human behavior and human culture and uses this to expand the meager sources that survive into a full blown reconstruction of some events. Indeed, Rushdie quotes his Cambridge Professor Hibbert saying "You must never write history until you can hear the people speak". Of course this is also the fundamental reason why histories of the same event written at various times in later centuries differ so much.
My personal experience reading Archimedes for the first time illustrates my bias: after getting past his specific words and the idiosyncrasies of the mathematical culture he worked in, I felt an amazing certainty that I could follow his thought process. I knew how my mathematical contemporaries reasoned and his whole way of doing math fit hand-in-glove with my own experience. I was reconstructing a rich picture of Archimedes based on my prior. Here he was working out a Riemann sum for an integral, here he was making the irritating estimates needed to establish convergence. I am aware that historians would say I am not reading him for what he says but am distorting his words using my modern understanding of math. I cannot disprove this but I disagree. I take math to be a fixed set of problems and results, independent of culture just as metallurgy is a fixed set of facts that can be used to analyze ancient swords. When, in the same situation, I read in his manuscript things that people would write today (adjusting for notation), I feel justified in believing I can hear him "speak".
Getting back to the Pythagorean rule, I think the first task is to ask why ancient peoples were led to study triangles. I think there are two interconnected and quite convincing reasons. One is that the value of a field depends on its area and for buying and selling and inheriting and taxing farms, the numerical value of this area is indispensable. Another is that as towns grew and became cities, the most convenient shape for buildings and for the street plan was a rectangle. In the first case, the natural method is to break the field up into approximate rectangles or right triangles. A right triangle is half a rectangle and a rectangle can divided into two right triangles by its diagonal. So you need to be able to lay out perpendicular lines and recognize when one corner of a triangle is a right angle, when a quadrilateral is a rectangle. In other words, the rulers of all ancient kingdoms needed skilled land measurers and master builders who knew some basic facts from geometry. This does not mean they required Pythagorean rule, but it suggests how useful it would be.
In Mesopotamia we are unbelievably lucky that records made in clay tablets, unlike records made on paper, papyrus, birch bark or string, are nearly permanent. Fire, for instance, makes clay more permanent instead of destroying it. We have a nearly three millennium record of clay tablets (and tokens) from Mesopotamia from which its cultural history can be reconstructed. Denise Schmandt-Besserat has used this data to construct a very convincing story of the origin of writing in the third millennium BCE Mesopotamia starting from clay tokens, then clay envelopes and finally cuneiform on solid clay tablets. Essentially, her theory says it all started from needing to say "Mr. so-and-so owns such-and-such". Their highly sophisticated place-value base 60 arithmetic seems to have originated from the need for a unified central accounting (perhaps in Ur III) including goods and labor which had been measured with many units often related by multiples such as 4,5,6,10,12 etc. Remarkable accounting tablets survive with detailed entries of labor and goods: see the book of Richard Mattessich on "The Beginnings of Accounting".
How about the measurement of land? The following wonderful paean to the Goddess Nisaba, who received literacy and numeracy as a wedding present from Enlil and passed it down to human beings, is found on one Babylonian tablet:
Nisaba, woman sparkling with joy,The "1-rod reed" and the "measuring rope" are the basic tools of the surveyor, here praised on a par with writing. Many "deed" tablets survive with plans of fields and measurements. But, in my way of thinking, the most impressive demonstration of their knowledge of Pythagoras is on the tablet MS 3049 in the Schøyen collection., which appears above in the sidebar. Here the authors calculate the distance in a gateway through a thick wall from e.g. the inner left bottom corner to the outer right top corner. Now Pythagoras ostensibly is a theorem about triangles -- but really it describes distances in Cartesian coordinates in 2 dimensions. Iterating it, one gets the distance in \( \mathbb R^n \) as the square root of the sum of the squares of each coordinate change: $$ d(\vec x,\vec y) = \sqrt{\sum_{i=1}^n (x_i-y_i)^2}$$ The great importance of Pythagoras's theorem is this Corollary. And here from Uruk in Babylon, sometime in the 17th century BCE, we find this used in 3-space.
Righteous woman, scribe, lady who knows everything:
She leads your fingers on the clay,
She makes them put beautiful wedges on the tablets,
She makes them sparkle with a golden stylus,
A 1-rod reed and a measuring rope of lapis lazuli,
A yardstick, and a writing board which gives wisdom:
Nisaba generously bestowed them on you.
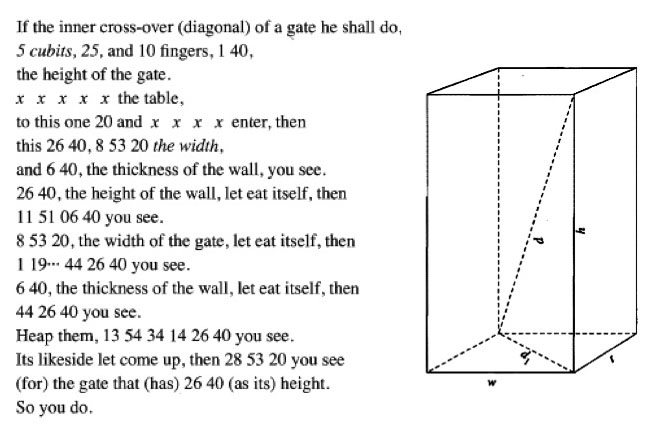On the left, a translation of the tablet from J. Friberg, "A Remarkable Collection of Babylonian Mathematical Texts"; on the right, his diagram of the calculation. Note that the numbers are in sexagesimal (so, for example, "6 40" means 6*60+40=400), "heap them" means add, "let eat itself" means square it, and "likeside" is its square root.
An aside: another tablet, Plimpton 322 which is in the sidebar to the home page of the site, is often used as evidence of the Mesopotamians' knowledge of the Pythagorean theorem, This contains a list of pairs \( (s,d) \) where \( d^2-s^2 \) is a square of an exact sexagesimal number \( \ell \) (i.e. of finite length) -- otherwise said, "Pythagorean triples" \( (s, \ell, d) \). As the tablet lists these for triangles with angles steadily decreasing from about 44 degrees to 32 degrees, it has been thought to be an equivalent of a table of sines or perhaps a manual for earthworks giving simple distances that could be laid out by surveyors. However, Eleanor Robson has proposed instead (in the American Math Monthly, Oct. 2001) that it was simply a table of reciprocal pairs \( (x,1/x) \) (now missing because the tablet broke) together with their sums and differences reduced to sexagesimally simple forms to simplify the work of setting problems, i.e. a teacher's manual. Its only hint of relating to triangles is that the heading of column of \( d \)'s is labelled "diagonal". But Schøyen 3049 explicitly uses the Pythagorean rule twice.
Who were the people who came up with this -- arguably the first "non-trivial" fact in mathematics? We know that there were scribal schools in which apprentices were trained in the three 'R"s, reading, (w)riting and (a)rithmetic, all highly skilled professions at the time. (Aside: besides arithmetic base 60 being quite a challenge, the script, like contemporary Japanese, was a mixture, in this case of Sumerian logograms and the Akkadian syllabic alphabet, hence another major challenge.) Bins of hundreds of discarded student tablets, many with errors, survive! Students in these schools became scribes working as bureaucrats, accountants, surveyors or teachers. But I contend that some scribes must have been mathematical geniuses too or the Pythagorean rule could not have been discovered. Should we think of them as the world's first mathematicians? There is some controversy here. For Eleanor Robson, all this work was oriented to engineering, administrative and instructional needs -- measuring and designing canals, earthworks, etc. and she asserts that thinking of them as mathematicians is a misguided anachronism that ignores the society in which they lived.
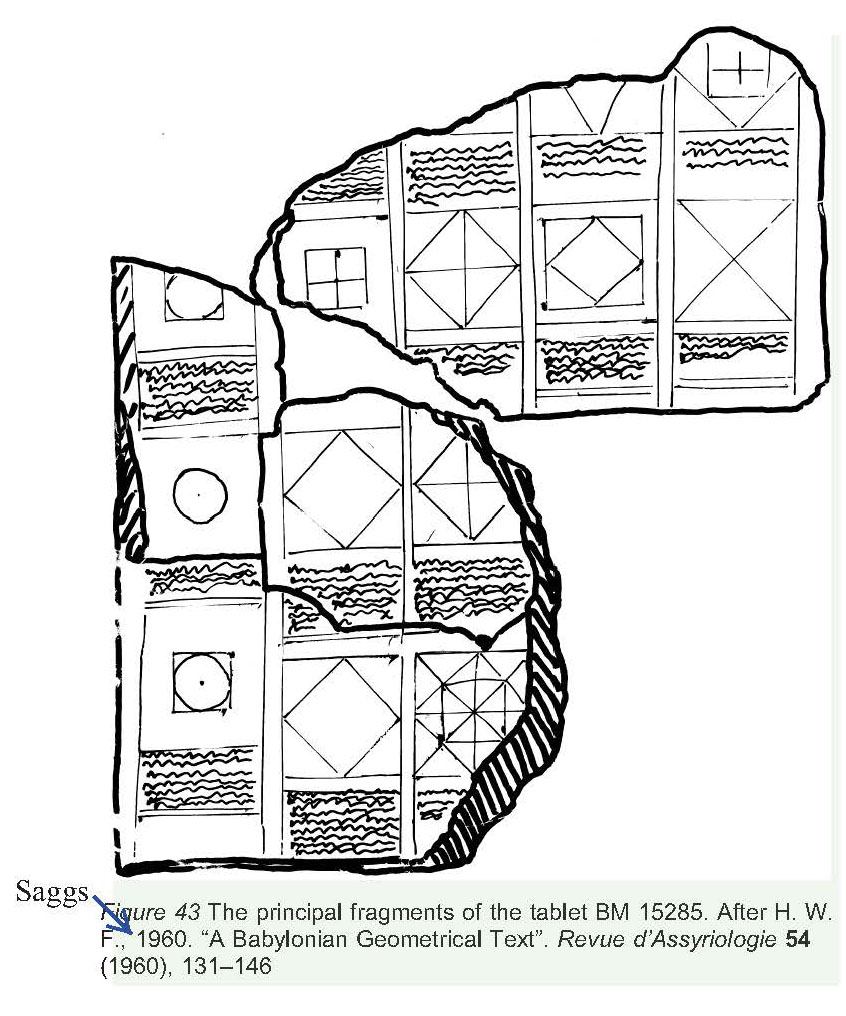
Perhaps this is just a reflection of the age-old tension between pure and applied mathematics. Many engineers have been mathematical geniuses. You don't have to be a professional mathematician to be a mathematical genius and it does seem a stretch to call anyone from that time a mathematician. Following Hibbert's dictum, let's imagine a brilliant civil servant whose day job was measuring fields or construction sites and writing tablets with associated plans but whose imagination was caught by these geometric diagrams and who then played with how these diagrams constrained lengths and areas (one might think of Einstein in the Swiss patent office). But how was the rule found? This is the real mystery. Jens Høyrup in his book "Length, Width, Surfaces: A Portrait of Old Babylonian Algebra and its kin" proposes, in connection his analysis of tablet Db2 146, that the Babylonians discovered a version of the famous Xian Tu diagram that appears in Chinese manuscripts of the Early Han dynasty (see below) that is also shown in the sidebar. The key to this diagram is to inscribe one square inside another at the angle that makes the gaps in the four corners all equal to the given triangle. Unfortunately, no trace of such a diagram has been found on a tablet. However, the case where the inner square is oriented at 45° is found on tablet BM 15285 shown in the sidebar. And once you conceive of this diagram, there are many ways to prove the rule. Høyrup, analyzing very carefully the exact words on tablet Db2 146, proposes one in his book, p.259, figure 67. Here's my favorite with \( A,B,C \) denoting the sides of the white triangles in the four corners:
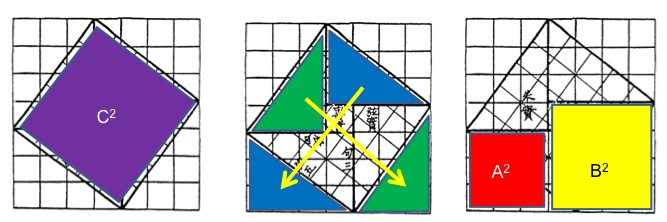
This begins to feel like a considerable speculative leap. But since Schøyen 3049 makes it unmistakable that somehow they found the result, I think we have to entertain such a speculation. But then did other cultures discover the result independently? Not necessarily: if we accept that Pythagoras's theorem and the accompanying geometry were very useful for taxes and building, it is only natural that its knowledge would spread to nearby civilizations with which Mesopotamia had regular trade. Master builders and surveyors would be in demand and some would likely migrate. Thus both Egypt and the Indus Valley culture flourished at pretty much the same time and so might learn of the latest technology from Babylon. Sadly, in both cases, we have much sparser remains from which to deduce what they knew. From Egypt, the so-called "Scorpion Macehead" shows the pharaoh seeding the fields adjacent to the Nile after its flood and is dated c.3000 BCE. To reconstruct the fields, "rope stretchers" were employed and paintings testify that knotted ropes were their principle tools. It is widely believed that they used the 3-4-5 triangle to lay out right angles for construction purposes. But the only evidence for this is problem 1 in the Berlin Papyrus 6619 where the equation \( x^2 + y^2 = 100, y/x=3/4 \) is solved. According to a recent review "Traditions and myths in the historiography of Egyptian mathematics" by Annette Imhaausen (in the Oxford Handbook of History of Math, p.791), judging from the mathematical papyri that have survived, it is doubtful that they knew the statement of the Pythagorean rule in general. Moreover, structures such as the great pyramid of Giza were built about 800 years before the above tablets were written. My guess is that, in the Old Kingdom, squares were laid out by using ropes to ensure that all sides were equal and both diagonals were equal. It's also plausible that the technique of laying out right triangles by a rope with knots at spaces 3, 4 and 5 could have been transmitted from Babylon during the Middle Kingdom while its theoretical background was not.
As for the Indus Valley culture, we have about 3700 inscriptions containing about 400 symbols but this is no help as they are still untranslated. But there are Sumerian descriptions of trade to a place in the East called "Meluhha", often identified with the Indus Valley, and identical clay seals are found in the Indus Valley and in Mesopotamia. Their cities were laid out with very regular rectangular street plans indicating their need for skilled surveying (as does the universal concern with fields). What makes the possibility of transmission of the full Pythagorean rule to the Indus valley a bit more plausible, however, is how the theorem crops up very explicitly in the Indian Vedic period, in the Sulba Sutra of Baudhayana, usually dated c. 800 BCE. Here the rule is used not for laying out fields, streets or buildings but for laying out sacrificial fire altars. The Vedic invaders of Northwest India are thought to have occupied the Indus Valley during the late periods of the Indus Valley culture and then spread East. How they interacted or interbred with the natives in this land and what, if anything, they picked up from them is the subject of great controversy. Regardless of where you stand on these sensitive issues, it is startling to find in Vedic Sutras not only the Pythagorean rule but the basic geometric constructions with ropes used in Mesopotamia and Egypt (and likely the Indus Valley): see figure above in the sidebar. If you put the Sulba Sutras next to a book on the geometry in the Mesopotamian tablets, the similarities are stunning. You might wonder why area was important to the Vedic peoples? There is a simple ritual reason: if a sacrifice did not achieve its aim, it was repeated, increasing the area of the altar by a ratio \( (n+1)/n \) for increasing values of n. If you use Pythagoras's rule, this is easy to do with ropes. We also find, a bit later, very sophisticated accounting used in the Maurya empire. All in all, it seems a reasonable speculation that a good deal of math was transmitted via the Indus Valley people to the Vedic Indians.
How about China? A key problem with the history of Chinese math is that mathematics and mathematicians never held an important place in Chinese culture. Math was a tool for low level bureaucrats and, in many dynasties, was not even part of the imperial exams. Astronomy and its sister, Astrology, held a somewhat higher place. But these were not esteemed as much as writing poetry and essays on Confucian ideals. After the massive burning of ancient documents and the burying alive of recalcitrant mandarins in the Qin dynasty, the Han dynasty scholars were able to reconstruct much of the ancient dynastic histories and Confucian manuscripts but only the final state of the math, not its history. Nonetheless, in what they reconstructed the Pythagorean rule emerges full blown. It occupies a full chapter in the main Han dynasty treatise, the "Nine Chapters on the Mathematical Art" (Jiu Zhang Suan Shu) and the proof using the Xian Tu appears in somewhat garbled form in the surviving late Zhou manuscript "Zhou Bi Suan Jing" (sometimes translated as the "Arithmetical Classic of the Gnomon").
Was this rule, as well as the use of Gaussian elimination and negative numbers to solve systems of linear equations, all discovered in the burst of creative activity in the Han dynasty? Chinese culture had expanded and built sophisticated societies with elaborate governments, earthworks etc. for over over a thousand years preceding the Qin. Confucius had lived three centuries earlier as had scientifically inclined philosophers like Mo Tzu. Although there is no direct evidence, it seems much more likely that Pythagoras's rule had been discovered sometime in the Zhou dynasty (1046-256 BCE, often subdivided into the Zhou proper, then the Spring and Automn period and finally the Warring States period). It also seems unlikely that its statement might have been transmitted from the Middle East in these early times. The culture of the Middle Kingdom has its own very distinct writing and founding myths. It seems most likely to me that another unsung mathematical genius discovered it in China in the early first millennium BCE.
Enough speculation. My central point is first that early math was applied math, embedded in practical tasks, especially accounting and surveying. Secondly, the algorithms in these fields can be transmitted to other cultures by their practitioners -- bureaucrats, scribes and master builders -- just as well as by the experts who first formulated them. But thirdly, for a few of these experts, the math they uncovered took on a life of its own, they pushed things to a deeper level and their discoveries, such as the Pythagorean rule, should be celebrated as much as those of metals and wheels. I think it is not anachronistic to call those experts mathematicians and I suspect they felt not unlike what my colleagues feel today when they find something new.
On Jan.10, Dick Palais wrote me the following comments:
The Pythagoras topic is one that has interested me for a long time, (for reasons that will appear below). What motivates me to write is a desire to convince you of my long held view that Pythagoras' Rule should be considered fairly superficial rather than ``deep'', and that certainly, when properly approached it is intuitively and mathematically almost obvious. Let me first give a quick outline and then add some further detail and discussion. Let's start by accepting:
Area Principle for Convex Polygons. The area of similar convex polygons is proportional to the squares of the lengths of corresponding sides. In particular, the areas of similar right triangles is proportional to the squares of the lengths of their hypotenuses.
Thus, given a right triangle \( T' \), there is a positive constant \( k \) such that, for any triangle \( T \) similar to \( T' \) and having a hypotenuse of length \( c \), the area of \( T \) equals \( k c^2 \). Now think of the hypotenuse of \( T \) as its base, and drop the perpendicular from the vertex of its right angle onto its base. This divides \( T \) into two non-overlapping triangles similar to \( T \) (and so to \( T' \)) whose hypotenuse lengths are the lengths, \( a \) and \( b \), of the two shorter sides of \( T \). Hence, by the additivity of area, \( k a^2 + k b^2 = k c^2 \), and dividing by \( k \) gives Pythagoras' Rule.
I suppose one might object that the Area Principle is not "obvious'" or elementary, but at least the special case, for right triangles is an immediate consequence of the proposition that "corresponding sides of similar triangles are proportional'", which I think most would agree is elementary. In fact, using the above notation, let \( a', b', c' \) be the three side lengths of a triangle \( T' \), so for \( T \) similar to \( T' \) with side lengths \( a,b,c \) we have \( {a\over a'} = {b\over b'} = {c\over c'} \). Now (by definition) the area of \( T \) and \( T' \) are respectively \( A(T) = {1\over 2} ab \) and \( A(T') = {1\over 2} a'b' \), so $$A(T) = A(T') {A(T)\over A(T')} = {1\over 2}(a'b') {a\over a'} {b\over b'} =\\ {1\over 2}(a'b') ({c\over c' })^2 = {1\over 2} \left({a'b' \over c'^2} \right) c^2 = k c^2$$ where \( k \) is the constant \( {1\over 2} \left({a'b' \over c'^2} \right) \), proving the special case of the Area Principle.
Now, while I think the above is all pretty "obvious'', I do not mean that I discovered it on my own (though I wish I had). What is true is that Einstein, in his autobiography, says that it is the proof that he discovered on his own, at age twelve, when his uncle challenged him to come up with a proof of Pythagoras Rule. And what I strongly suspect is also true is that many different ancient geometers from various cultures in the far past stumbled upon this argument, and perhaps you should take the above into account in your Bayesian analysis, particularly in view of your remark: "I think there are two interconnected and quite convincing reasons. One is that the value of a field depends on its area and for buying and selling and inheriting and taxing farms, the numerical value of this area is indispensable."
I agree this is a great proof. It is essentially in Euclid's book VI, specifically VI.8 and VI.19 though Euclid doesn't explicitly note that it reproves the Pythagorean rule. I just doubt that this was the route by which it was first discovered, being a pretty abstract approach. It strongly depends on the general notion of similarity as well as the quadratic dependence of area on size. This level of abstraction first appears in Greek math. Depending on how much abstraction one likes, one can also argue that rotations must be linear and that compact one-parameter subgroups of GL(2,R) leave invariant a quadratic form. This is rather like Grothendieck's belief that when you have a sufficiently high level understanding of math, the concrete classical results will fall out.
Dick replied: "Gee, I felt it was more concrete and natural than say the one involving the Xian Tu diagram. Chacun à son goût I guess." He is using "natural" the way all professional mathematicians do -- namely natural from their higher perspective. I think the Xian Tu is more elementary: you just shuffle blocks around.
Marius Kempe wrote me drawing my attention to Christopher Cullen's article in the AMS Notices. Cullen argues on the basis of the slim surviving source material from the Han dynasty that it is unlikely that the Pythagorean rule was known any earlier:
His conclusion: the rule was unknown in China before roughly the first century BCE. I feel this is exactly the main problem with standard historical scholarship. Why assume that the surviving sources describe well the full state of knowledge at that point in space-time? Specifically, why assume that the above mentioned manuscript, the Suan Shu Shu found in a tomb, contains a comprehensive survey of contemporary mathematical knowledge? We know that the Qin leaders systematically burned older manuscripts and killed mandarins and this caused a big problem for the Han dynasty in rebuilding their culture. Getting down to the brass tacks of his argument, Cullen translates the key passage in the possibly much older Zhou Bi Suan Jing on p.786 of his article in order to refute the admittedly creative translations that aim to show it contains a description of the Xian diagram that establishes the Pythagorean rule. But his translation is equally mysterious to me because he gives no diagram to explain it. If he had translated it so as to give a more pedestrian sense to the passage, he might have an argument. Such details aside, I feel the strongest argument for earlier Chinese knowledge of the rule is the long history of their culture, their cities and their civil works. It would seem bizarre if they failed to find this rule, one that was widely used in all other cultures that attained this level.A manuscript of a pre-canonical mathematical text recently found in a tomb of the second century B.C. does not make use of the gougu (=Pythagorean) relation, even where one might have expected to find it, in problems relating to sawing a square beam out of a round log. So it seems that we have at least a rough fix on when gougu thinking began in China.
On May 27, I had an interesting exchange with Jonathan Crabtree in Melbourne. He first wrote in connection my paper on negative numbers that Euclid's definition in Book VII of multiplication of positive integers is always misleadingly translated, ignoring the fact that Euclid was really dealing with line segments. Thus, he says Euclid did not say "a.b means add a to itself b times" but rather "a.b means a put together b times". That is, line segments can be put together, extending them along the line containing one of them and this is a tangible operation on the segments, not to be identified with the binary operation of addition. He then wrote me on the above blog too:
As a rule, I do not like the trend that says Euclid knew algebra because we can interpret geometry algebraically today. Yet we can revisit the past and say, based on what we know now, we can also do this...
It is easy to read far too much into the Sanskrit of Brahmagupta for example. Then people say Brahmagupta defined a negative number as a positive number subtracted from zero. That may be the case, yet Brahmagupta did NOT say it!
"Pythagoras ostensibly is a theorem about triangles." Yet the circle on the hypotenuse equals the sum of the circles on the other two sides. From triangles to squares is one step, yet why has nobody written about the beauty of from triangles to circles? Yes, area, land and tax lead to a preference for squares on sides, not any of the other shapes that follow the same principle.
"Math was a tool for low level bureaucrats " Same in Greece and India. Arithmetica was number theory not the application of numbers to objects. (Arithmoi vs arithmos?) In India practical math was called logistics and associated with engineering.
The Chinese did NOT have negative numbers that mean a number is less than zero. They had opposite units that were both counted with the same numbers. So the red and black rods counted opposite things such as debts and assets or income and expense. As in India, numbers of objects jumped to the opposite unit upon reaching zero-India or empty-China.
The West fell for the trap of numbers less than zero only because of a focus on the right hand side of the number line and religious baggage associated with zero infinity and less than zero, which challenged the Church.
As for the comment of Roy Smith on this post, just two days ago I created this applet http://tube.geogebra.org/student/m1242381 which Steiner wrote about and Euclid proved in III P36.
As for Roy's last question proportion is at the heart of universal mathematics - not just because of Thales. I did a word count to compare additive words with proportional words in Newton's Principia. The results are at http://www.jonathancrabtree.com/mathematics/master-key-unlocks-science-addition-proportion/.
Now I must finish my applet showing Pythagoras with circles...http://tube.geogebra.org/student/m1256107
A couple of replies: first, the Vedic Indians needed to scale up complex shaped altars so that their area increased by a factor \( (n+1)/n \) and these shapes were sometimes approximations to circles (not exact because they were made of rectangular bricks). So this extension of the Pythagorean rule would not surprise them.
Second, if you can add, subtract and multiply mixed expressions of positive and negative numbers, it seems a quibble to say that because you made them red and black, you did not think of them as part of one number system.
