THE CRUNCH GROUP
Division of Applied Mathematics
Brown University
Providence, RI 02912, USA




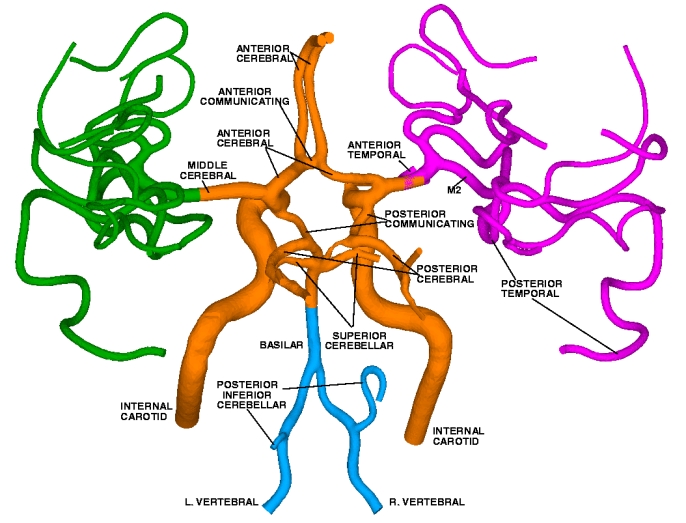
Two-level Domain Decomposition MethodThe emerging generation of petaflop supercomputers permits deeper insight into physiological phenomena. From the computational standpoint, it makes feasible the solution of a problem with billions of unknowns in reasonable time. However, a straight-forward approach in simulating 3D flow in the Macrovascular Network is computationally prohibitive even on petaflop computers, due to extremely large size of tightly coupled problem and high cost of communication over thousands of processes. In order to exploit the available computational resources efficiently, and make progress in understanding the physiology of the arterial system we develop a new ultra-parallel paradigm. A new two-level method for the Navier-Stokes equations we develop combines the best features of discontinuous and continuous Galerkin formulations. According to the method the large computational domain is first subdivided into overlapping patches (coarse level partitioning); within each patch a spectral element discretization (fine level) is employed. An example of large Macrovascular Network reconstructed from MR images of the brain is presented in the figure bellow.
The overall scalability of the method depends on the strong scaling within a patch and the weak scaling in terms of the number of patches. This dual path to scalability provides great flexibility in balancing accuracy and parallel efficiency. Performance of NektarG on CRAY XT5 (Kraken) of NICS, University of Tennessee .
Performance of NektarG on BlueGene/P (Intrepid) of ALCF ANL.
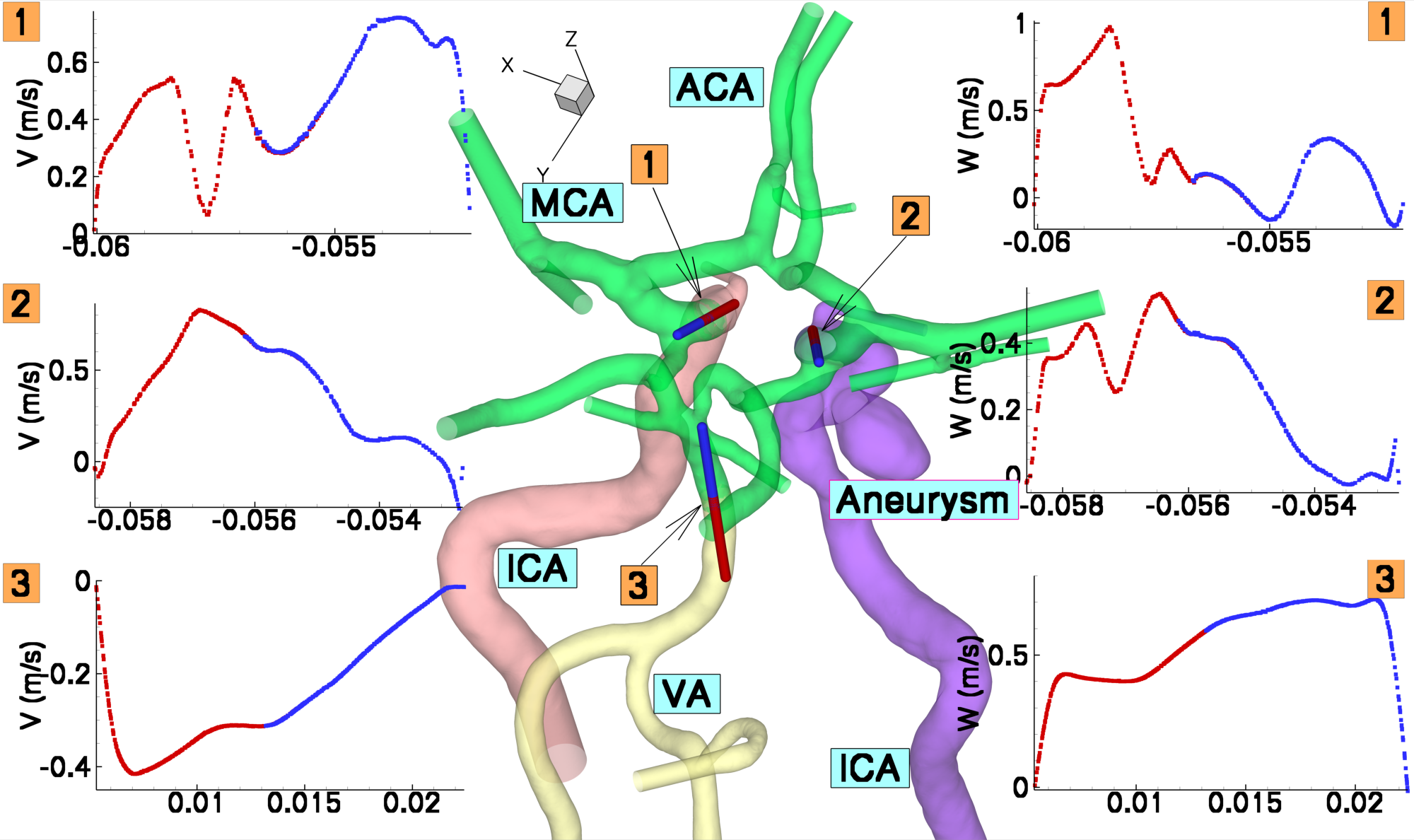
The method has been implemented in unsteady flow simulation in major arteries of the brain. In the figure bellow the computational domain constructed from four overlapping patches is presented. In the XY plots we plot the velocity profile extracted across the overlapping regions (along the red-blue lines marked by 1,2 and 3).
|
||||||||||||||||||||||||||||||||||||||||||||||
Publications
|