JGemmer

Welcome	Research	Publications	Teaching	CV

In 1696 Johann Bernouli introduced one of the first modern variational problems by posing the following Brachistochrone problem: "Find the shape of the curve down which a bead sliding from rest and accelerated by gravity will fall from one point to another in the least time." For uniform gravitational fields, Sir Isaac Newton, Gottfried Leibniz, Guillaume De L’Hospital, Jakob Bernouli, and Johann Bernouli used rudimentary techniques from the calculus of variations to show that the that the solution is a cycloid, the curve traced out by a point on the rim of a rolling circle. Today variational problems arise in a number of areas including nonlinear elasticity, image processing, pattern formation, liquid crystals, and phase transitions. The calculus of variations is an indispensable tool for studying such problems and is fascinating topic to study in its own right. In generalized brachistochrone problems we are interested in studying this problem for various gravitational fields and geometries.

Below are some movies that illustrate Brachistochrone solutions for particles falling in uniform graviational fields, inverse square graviational fields, and on hyperboloids of revolution lying in uniform graviational fields.

Uniform Gravitational Field

Inverse Square Gravitational Field

Hyperboloid of Revolution

Undergraduate Student Research Project:

In this project the student will be introduced to variational problems by using the calculus of variations and direct methods to study the Brachistochrone problem in inverse square gravitational fields. This problem can be thought of as constructing Brachistochrone solutions on the scale where the Earth (or the sun) is small compared with the distance travelled by the particle.

Interestingly, in the inverse square case the solutions to these differential equations do not span the entire domain. Specifically, there is a sector of angular width \(2\pi/3\) that can not be reached by a classical solution to the Euler-Lagrange equations. That is, given two points A and B there may not exist a solution in the classical sense to the Euler-Lagrange equations connecting these two points. This is a curious result that seemingly indicates that there does not exist a curve of minimum time connecting these two points. This result is illustrated in the figure below where exact solutions to the Euler-Lagrange equations for an inverse square gravitational field are plotted.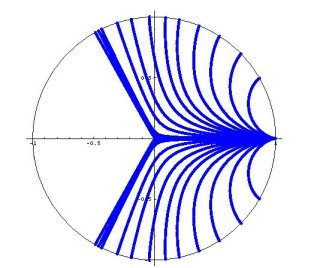

The initial goal of the project will be for the student to use direct numerical minimization routines to construct discrete approximations to minimizers of the problem. Specifically, the student will use a finite difference scheme to create a discrete version of the problem which can then be directly minimized. In this discrete setting a minimum curve exists for all points A and B and as the number of points in the discretization goes to infinity these approximate solution curves will converge to a continuous, but perhaps not differentiable curve. Through this numerical study the student will gain insights as to why the solutions to the Euler-Lagrange equation fail to adequately describe minimizers of the Brachistochrone in the inverse square case. Furthermore, the numerical results will guide future work in formulating an analytic solution to the problem.

In this project the student will provide a solution to an open problem in the calculus of variations, namely what continuous curves solve the Brachistochrone problem for an inverse square gravitational field. While this research is interesting its own right, this work will ultimately serve as an educational project from which the student will learn how to derive and solve the Euler-Lagrange equations for a variational problem, how to construct finite difference approximations, how to program in a high level mathematical programming software such as Matlab or Mathematica, how to give mathematics presentations, and how to write mathematics at a publication level quality. Moreover, the student will gain an understating and appreciation for what is involved in research in applied mathematics and will be prepared to conduct research in graduate school or in the private sector.