Matt Harrison

Current Research

Overview

My group is currently studying statistical methods that are agnostic about certain aspects of the underlying distribution of the data. This seems increasingly desirable in many modern problems because of the inherent difficulties that arise when modeling high-dimensional distributions. Applications in neuroscience are an area of special focus. Here we would like statistical methods that can resolve scientific questions about processes operating on a given time scale, while being agnostic about processes operating at different time scales.

Some of the interesting side projects that have arisen along the way include sampling algorithms for graphs with specified degree sequences (or tables with specified margins), a simple procedure to provably control the type I error rate of Monte Carlo hypothesis tests based on importance sampling, and improved algorithms for brain-machine interfaces for people with tetraplegia.

---

Estimating the number of components in a finite mixture

People

• Jeff Miller
• Matt Harrison

Presentations and Manuscripts

• J Miller, M Harrison. A simple example of Dirichlet process mixture inconsistency for the number of components. arXiv:1301.2708.
• J Miller, M Harrison (2012) Posterior consistency for the number of components in a finite mixture. 2012 NIPS Workshop on Modern Nonparametric Machine Learning. Lake Tahoe, NV.
• J Miller, M Harrison (2012) Dirichlet process mixtures are inconsistent for the number of components in a finite mixture. ICERM Bayesian Nonparametrics Workshop. Providence, RI. Slides [pdf]

Summary

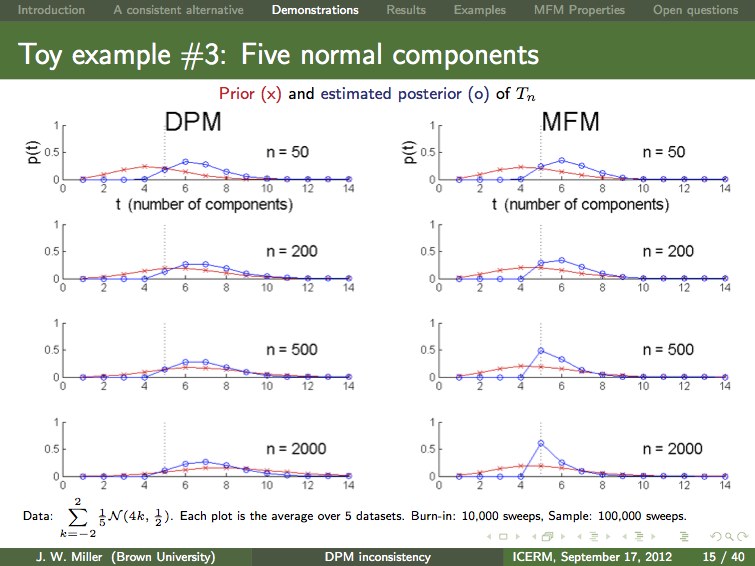
Dirichlet process mixtures (DPMs) are often applied when the data is assumed to come from a mixture with finitely many components, but one does not know the number of components s. In many such cases, one desires to make inferences about s, and it is common practice use the posterior distribution on the number of components occurring so far. It turns out that this posterior is not consistent for s. That is, we have proven that given unlimited i.i.d. data from a finite mixture with s₀ components, the posterior probability of s₀ does not converge to 1. The same result holds for Pitman-Yor process mixtures, and many other related nonparametric Bayesian priors. Motivated by this finding, we examine an alternative approach to Bayesian nonparametric mixtures, which we refer to as a mixture of finite mixtures (MFM). In addition to being consistent for the number of components, MFMs are very natural and possess many of the attractive features of DPMs, including: efficient approximate inference (with MCMC), consistency for the density (at the optimal rate, under certain conditions), and appealing equivalent formulations ("restaurant process", distribution on partitions, stick-breaking, and random discrete measures). Our findings suggest that MFMs are preferable to DPMs when the data comes from a finite mixture.

Here's a slide from Jeff's ICERM presentation comparing inference in a toy example. The posterior (blue curve) is not concentrating around the true number of components (s₀=5) for the DPM (left), but it is for the MFM (right). More data does not change things -- the DPM posterior is not consistent, but the MFM posterior is consistent. Forcing the DPM prior to remain stable by varying the concentration parameter with the amount of data does not help (not shown). Pruning small components does appear to help (not shown), but we do not have a proof, and using MFMs instead of DPMs seems more natural in this case.

 

---

Conditional inference algorithms for graphs and tables

People

• Matt Harrison
• Jeff Miller
• Dan Klein

Presentations and Manuscripts

• J Miller, M Harrison (2013) Exact sampling and counting for fixed-margin matrices. arXiv:1301.6635.
• M Harrison, J Miller. Importance sampling for weighted binary random matrices with specified margins. arXiv:1301.3928.
• J Miller, M Harrison. Exact enumeration and sampling of matrices with specified margins. arXiv:1104.0323.
• M Harrison (2012) Conservative hypothesis tests and confidence intervals using importance sampling. Biometrika, 99: 57-69. [See example 4.2.]
• J Miller, M Harrison (2010) A practical algorithm for exact inference on tables. Proceedings of the 2010 Joint Statistical Meeting.
• J Miller, M Harrison (2011) A practical algorithm for exact inference on tables. New England Statistics Symposium 2011. Storrs, CT.
  IBM Thomas J. Watson Research Center Student Research Award
• M Harrison. A dynamic programming approach for approximate uniform generation of binary matrices with specified margins. arXiv:0906.1004.

Summary

We are studying the conditional distribution of independent integer-valued random variables arranged in a matrix given the sequences of row and column sums (the margins). An important special case is the uniform distribution over binary matrices with specified margins.

• Exact enumeration and sampling. We have developed an algorithm for exact enumeration and exact iid uniform sampling from the set of binary matrices (and also nonnegative integer matrices) with specified row and column sums (arXiv:1301.6635). The uniform distribution arises as a null distribution in ecology (for testing species co-occurrence matrices), in educational testing (for goodness of fit tests for the Rasch model), and in network analysis (as a null model for bi-partite graphs). Our algorithm is practical in many real-world examples, particularly those arising in ecology. For example, here is a famous dataset from ecology (Patterson and Atmar, 1986) with entry (i,j) indicating the presence of species i in habitat j:
   
  

   1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
   1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0
   1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 1
   1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 0 1 0 0 0 0
   1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 0 1 0 0 0 0
   1 1 1 1 1 0 0 0 1 1 1 1 1 0 1 1 0 1 1 1 1 0 1 0 1 0 0 0
   1 1 1 1 1 1 1 0 1 1 1 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 1 0 1 1 0 1 0 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 1 1 1 0 1 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 1 1 1 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 0 0 1 1 0 0 0 1 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0
   1 1 1 1 1 0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 0 1 1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 0 1 1 1 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   
  

  We find that the number of binary matrices with the same margins as this matrix is the 40 digit number 2663296694330271332856672902543209853700, and we can efficiently generate iid uniform samples from this set.
   
• Importance sampling. We have also developed an importance sampling algorithm for the uniform distribution over binary matrices with specified margins (arXiv:0906.1004). It takes about a minute to generate 100,000 importance samples in the ecology example above, giving an approximation of (2.644±0.035)×10³⁹, which is close to the true value. (We are reporting the point estimate ± twice the approximate standard errors.) Importance sampling can scale to much larger examples. For example, we approximate the number of 1000×1000 binary 512-regular matrices (meaning all row and column sums are 512) to be (5.02208±0.00014)×10²⁹⁷⁷¹¹ based on 1000 importance samples. The ratio of maximum to minimum importance weights in this case is 1.004, which is striking.

 

---

Conservative hypothesis tests and confidence intervals based on importance sampling;
Accelerated multiple testing based on importance sampling

People

• Matt Harrison

Presentations and Manuscripts

• M Harrison (2013) Accelerated spike resampling for accurate multiple testing controls. Neural Computation, 25: 418-449.
• M Harrison (2012) Conservative hypothesis tests and confidence intervals using importance sampling. Biometrika, 99: 57-69.
• M Harrison (2011) Importance sampling for accelerated multiple testing and confidence intervals. New England Statistics Symposium 2011. Storrs, CT.

Summary

In many cases p-values for a hypothesis test can be approximated by Monte Carlo methods. The resulting approximate p-values are just that: approximate. They need not control the type I error rate at the nominal level. There are two cases where this is a big deal: (1) if the Monte Carlo sampling algorithms have high variability, so that the approximation errors could be large; or (2) if one wishes to adjust the p-values to account for multiple hypothesis tests, which usually causes the approximation errors to get greatly magnified. This work shows how to easily create Monte Carlo p-values using importance sampling that, although still approximations of the original p-value, nevertheless control the type I error rate at the nominal level. I would argue that this technique should always be used when reporting p-values based on importance sampling. Interesting applications include (1) the construction of Monte Carlo confidence intervals that preserve the nominal coverage probabilities, and (2) accelerated Monte Carlo multiple testing, including neuroscience applications.

 

---

Robust inference for lag-lead relationships in multivariate binary time series;
Inferring the cortical microcircuitry from spike train data

People

• Matt Harrison
• Dahlia Nadkarni
• Han Amarasingham (CCNY)
• Neurophysiologists and Computational Neuroscientists: Gyuri Buzsaki (NYU), Shige Fujisawa (RIKEN)

Presentations and Manuscripts

• M Harrison (2013) Accelerated spike resampling for accurate multiple testing controls. Neural Computation, 25: 418-449. [See the real-data example.]
• D Nadkarni, M Harrison (2012) The incidental parameter problem in network analysis for neural spiking data. 2012 Women in Machine Learning Workshop. Lake Tahoe, NV.
• M Harrison (2012) Conditional Inference for Learning the Network Structure of Cortical Microcircuits. 2012 Joint Statistical Meeting (JSM). San Diego, CA.
• M Harrison (2012) Learning the Network Structure of Cortical Microcircuits using Conditional Inference. 8th World Congress in Probability and Statistics. Istanbul, Turkey.
• M Harrison (2012) Incidental parameter problems arising from the analysis of nonstationary neural point processes. New England Statistics Symposium 2012. Boston, MA.
• M Harrison, S Geman (2011) Learning the network structure of cortical microcircuits. IMA Workshop on Large Graphs: Modeling, Algorithms and Applications. Minneapolis, MN. [abstract] [video lecture]
• S Fujisawa, A Amarasingham, M Harrison, G Buzsaki (2008) Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nature Neuroscience, 11: 823-833.

Summary

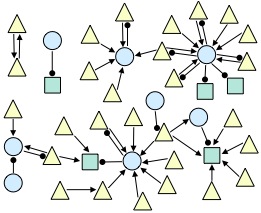
The spiking electrical activity of many synaptically coupled neurons can reveal evidence about their underlying circuitry. Statistical approaches to inferring this circuitry are hampered by the myriad of other processes that influence neural firing. We are exploring conditional inference as a promising tool for addressing these challenges. This is joint work with CCNY Professor Han Amarasingham and in collaboration with Professor Gyuri Buzsaki's neurophysiology lab at NYU and Professor Shige Fujisawa's neurophysiology lab at RIKEN. The figure below shows an example network inferred from data recorded from the prefrontal cortex of an awake, behaving rodent (triangle=excitatory; circle=inhibitory; square=unknown).

 

---

Jitter: Conditional inference for disambiguating time scales in neurophysiological point processes

People

• Matt Harrison
• Han Amarasingham (CCNY)
• Stu Geman (Brown)
• Neurophysiologists and Computational Neuroscientists: Wilson Truccolo (Brown), Nicho Hatsopolous (Chicago), David Sheinberg (Brown), Britt Anderson (Waterloo)

Presentations and Manuscripts

• M Harrison, A Amarasingham, R Kass (in press) Statistical identification of synchronous spiking. In, Spike Timing: Mechanisms and Function. Editors: P Di Lorenzo, J Victor. Taylor & Francis.
• M Harrison (2013) Accelerated spike resampling for accurate multiple testing controls. Neural Computation, 25: 418-449.
• M Harrison, S Geman (2011) Learning the network structure of cortical microcircuits. IMA Workshop on Large Graphs: Modeling, Algorithms and Applications. Minneapolis, MN.
• M Harrison, S Geman (2009) A rate and history-preserving resampling algorithm for neural spike trains. Neural Computation, 21: 1244-1258.
• S Fujisawa, A Amarasingham, M Harrison, G Buzsaki (2008) Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nature Neuroscience, 11: 823-833.
• B Anderson, M Harrison, D Sheinberg (2006) A multielectrode study of IT in the monkey: Effects of grouping on spike rates and synchrony. NeuroReport, 17: 407-411.
• M Harrison, A Amarasingham, S Geman (2007) Jitter methods for investigating the time scale of dependencies in neuronal firing patterns. 2007 Joint Statistical Meeting (JSM). Salt Lake City, UT.
• A Amarasingham, M Harrison, S Geman (2007) Jitter methods for investigating spike train dependencies. Computational and Systems Neuroscience (COSYNE) 2007. Salt Lake City, UT.
• M Harrison, A Amarasingham, S Geman (2006) Statistical methods for non-repeatable observations in neuroscience. ICSA 2006 Applied Statistics Symposium. Storrs, CT.
• A Amarasingham, M Harrison, S Geman (2006) Statistical analysis of neuronal firing patterns with non-repeatable trials. 3rd Workshop on Statistical Analysis of Neuronal Data (SAND3). Pittsburgh, PA.
• B Anderson, M Harrison, D Sheinberg (2006) Neuronal synchrony and visual grouping: A multi-electrode study in monkey IT. Journal of Vision, 6(6):65, 65a.
• A Amarasingham, M Harrison, S Geman (2005) Statistical techniques for analyzing nonrepeating spike trains. Annual Society for Neuroscience Meeting (SFN) 2005. Washington, DC.
• M Harrison (2005) Discovering compositional structures. PhD Dissertation. Brown University.

Summary

This has been a research topic of mine for many years, beginning (for me) with parts of my PhD dissertation under the supervision of Stu Geman and in collaboration with Han Amarasingham (also a former student of Stu Geman). The idea has matured significantly in recent years and is a direct precursor to our work on inferring lag-lead relationships in spike trains. The gist of the idea is summarized in this figure:

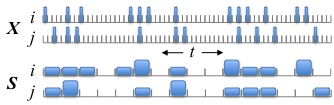
The original spike train data is X, with neurons i and j, and each 1 ms time bin records the number of spikes in that time bin. We can easily see that neuron j tends to fire 2 ms (time bins) after neuron i. If we had used 4 ms time bins (shown in S), then that information about precise spike timing appears to be obscured. However, before asserting that the relationship between the spikes is precisely timed, we should check to make sure that S doesn't encode this apparently precise relationship between between i and j. Of all possible spike trains that are consistent with S, what fraction have most of neuron j's spikes following exactly 2 ms after neuron i's spikes? If this fraction is small, then we would conclude the spikes are indeed precisely timed. But if this fraction is large, then we prefer to withhold judgement: the apparent precise timing can be easily explained by coarser modulations in firing rate. The name "jitter" comes from the observation that a randomly chosen spike train subject to S can be created by randomly perturbing (or jittering) the original spike times within their respect coarse time bins. Much of our original work was motivated by neurophysiological questions related to synchrony, i.e., zero-lag alignments of spikes, instead of the nonzero lags in the above example.