Table of Contents
CRUNCH Fractional PDEs Club
The Fractional PDEs Club at CRUNCH group aims to formulate robust and efficient methods for deterministic and stochastic fractional PDEs (FPDEs) under the supervision of Prof. George Em Karniadakis. This is done through the development of a variety of numerical methods such as finite-difference methods, spectral methods, spectral element methods, and discontinuous Galerkin (DG) methods. We host the FPDEs Club meeting to provide opportunities for enhanced exchanges of ideas and cooperation among the FPDEs community, inside and outside of the FPDEs club.
Fractional PDEs
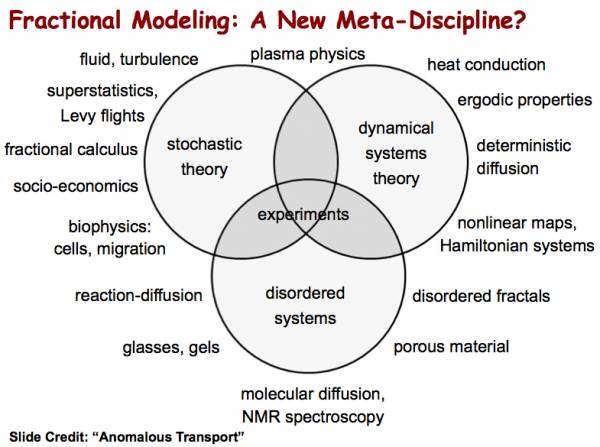
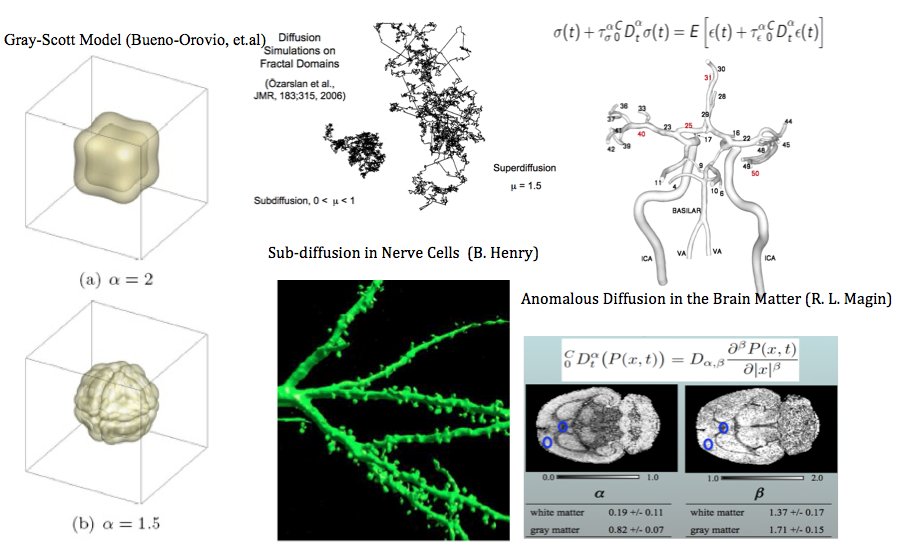
Fractional PDEs (FPDEs) generalize the standard (integer-order) calculus and PDEs to any differential form of fractional orders. FPDEs are emerging as a powerful tool for modeling challenging multiscale phenomena including overlapping microscopic and macroscopic scales, anomalous transport, and long-range time memory or spatial interactions. The fractional order may be a function of space-time or even be a distribution, opening up tremendous opportunities for modeling and simulation of multiphysics phenomena, e.g. seamless transition from wave propagation to diffusion, or from local to non-local dynamics. It is even possible to construct data-driven fractional differential operators that fit data from a particular experiment or specific phenomenon, including the effect of uncertainties, in which the fractional orders are determined directly from the data! In other words, a new (and simple) data assimilation problem can be formulated to determine the fractional order (or possibly a distribution) through taking into account diverse sources of information, including all available experimental data albeit of variable fidelity.
Applications
There is now an extensive amount of experimental evidence indicating that such phenomena occur in many applications in mechanics, including non-Gaussian (Levy) processes in turbulent flows, non-Newtonian fluids and rheology, non-Brownian transport phenomena in porous and disordered materials, and non-Markovian processes in multi-scale complex fluids and multi-phase applications. Moreover, there exist many other critical applications in biomechanics, such as anomalous thermo-fluid processes in human brain, nonlocal viscoelasticity in human red-blood-cells, and power-law stress relaxation in wall-arteries. In such applications, fractional PDEs naturally appear as the right governing equations leading to high-fidelity modeling and predictive simulations, which otherwise cannot be achieved using the standard PDEs.
Conferences
Fractional PDEs: Theory, Algorithms, and Applications, ICERM (Brown University), Providence, RI, June 18 - 22, 2018
Courses
Short Course on FPDEs:
Hong Wang, University of South Carolina
Introduction to fractional partial differential equations: Modeling, computation, and analysis
Part I: From Normal to Anomalous Diffusion (April 12)
Part II: Computational Issues of FPDEs (April 19)
Part III: Mathematical Issues of FPDEs (April 26)
MURI
Current MURI on Fractional PDEs for Conservation Laws and Beyond: Theory, Numerics, and Applications
FPDE Researchers World-Wide
To suggest researchers who should be added to this list, please contact anna_lischke(at)brown(dot)edu.
Data
The following data files are results from an investigation of the transport of nonreactive tracers in a saturated, heterogeneous aquifer which are not intended for distribution and are password-protected. Researchers in our research group may gain access to these files by emailing anna_lischke(at)brown(dot)edu.
Reference Materials
Links
Lorentz Center Workshop on Fractality and Fractionality, May 17-20, 2016, Leiden, Netherlands
The First International Symposium in Fractional PDEs in the United States
Short Course on Fractional PDEs
International Symposium on Fractional PDEs: Theory, Numerics, and Applications
FPDEs Club's Favorite Books:
Members
Prof. George Karniadakis
Prof. Mark Ainsworth
Can Huang
Wei Cai
Prof. Wanrong Cao
Fangying Song
Prof. Mohsen Zayernouri
Fanhai Zeng
Prof. Zhongqiang (Handy) Zhang
Xuan Zhao
Anna Lischke
Jorge Suzuki
Zhiping Mao
Xiaoning Zheng
Mamikon Gulian
Christian Glusa
Xuejuan Chen
Guofei Pang
Supervisor
Presentations
[76] Mamikon Gulian, “Fractional Path Integral Monte Carlo”
[75] Anna Lischke, “What is the fractional Laplacian?”
[74] Zhiping Mao: “Discretisations of the spectral fractional Laplacian on general domains with Dirichlet, Neumann, and Robin boundary conditions” by Cusimano, Del Teso, Gerardo-Giorda, and Pagnini.
[73] Xuanjuan Li: “Spectral methods for the Volterra integral equations”
[72] Fangying Song: “Turing Patterns in the Legnyel-Epstein System with Superdiffusion” by Liu, Wu, and Iqbal.
[71] Professor Weihua Deng: “Open Issues in Boundary Conditions of FPDEs and the Generalized Feynman-Kac Equation”
[70] Fangying Song: “A generalization of the Becker model in linear viscoelasticity: creep, relaxation, and internal friction” by Mainardi, Masina, and Spada.
[69] Mamikon Gulian: “Normal and Anomalous Diffusion: A Tutorial” by Loukas Vlahos, Heinz Isliker, Yannis Kominis, and Kyriakos Hizanidis.
[68] Zhiping Mao, Title: “DG method for pressureless Euler equation with nonlocal flocking”.
[67] Mehedi Hasan, Title: “Nonlinear response of a beam governed by fractional derivatives”.
[66] Anna Lischke, Title: “High-Order Accurate Adaptive Kernel Compression Time-Stepping Schemes for Fractional Differential Equations” by Daniel Baffet and Jan Hesthaven.
[65] Fangying Song, Title: “Error Analysis of a High Order Method for Time-Fractional Diffusion Equations” by Chunwan Lv and Chuanju Xu.
[64] Mehedi Hasan, Title: “Numerical Methods for Solving Fractional Optimal Control Problems”.
[63] Fangying Song, Title: “Fast algorithm for the space-time fractional diffusion equation”.
[62] Xuejuan Chen, Title: Numerical dissipativity and contractivity of finite difference schemes for fractional ODEs.
[61] Mamikon Gulian, Title: “Basics of control theory”.
[60] Anna Lischke and Mamikon Gulian, Title: “A Laplace transform method for the time-fractional Burgers' equation”.
[59] Zhiping Mao, Title: “Finite element method for Riesz fractional diffusion equation on irregular domain” by Weiping Bu.
[58] Fangying Song, Title: “Numerical methods for the fractional Fokker-Planck equation.”
[57] Mamikon Gulian and Brenda Rubinstein, Title: “Condensates in fractional quantum mechanics”.
[56] Mehedi Hasan, Title: “From continuous time random walks to the fractional Fokker-Planck equation” by E. Barkai, R. Metzler, and J. Klafter.
[55] Xuan Zhao and Beichuan Deng, Title: “Superconvergence points of fractional spectral interpolation” by Xuan Zhao and Zhimin Zhang.
[54] Guofei Pang, Title: “Multi-variate Gaussian process regression for fractional inverse problems”.
[53] Fanhai Zeng, Title: “Fast convolution for nonreflecting boundary conditions” by C. Lubich and A. Schadle.
[52] Paris Perdikaris, Title: “Fractional Modeling of Viscoelasticity in 3D Cerebral Arteries and Aneurysms”.
[51] Mehedi Hasan, Title: “Fox H-functions and their applications in Fractional Calculus”.
[50] Xuejuan Chen, Title: “A tunable finite difference method for fractional differential equations with non-smooth solutions” (Update)
[49] Zhiping Mao, Title: “Fractional Quantum Mechanics” by Nick Laskin.
[48] Fangying Song, Title: “Finite element methods for Riesz space fractional diffusion equations”.
[47] Prof. Changpin Li, Title: “Finite element calculations of some typical fractional partial differential equations”.
[46] Anna Lischke, Title: “On Volterra functions and Ramanujan integrals” by Garrappa and Mainardi.
[45] Mamikon Gulian, Title: “A class of second order difference approximations for solving space fractional diffusion equations” by Tian, Zhou, and Deng.
[44] Xuejuan Chen, Title: “A tunable finite difference method for fractional differential equations with non-smooth solutions”.
[43] Zhiping Mao, Title: “Fast solvers for finite volume methods”.
[42] Fangying Song, Title: “Approximate the fractional Laplacian”.
[41] Dongkun Zhang, Title: “Data-driven uncertainty quantification using the arbitrary polynomial chaos expansion” by S. Oladyshkin and W. Nowak.
[40] Mamikon Gulian, Title: “Finite difference approximations for fractional advection–dispersion flow equations” by Meerschaert and Tadjeran.
[39] Victor Suriel, Title: “Eulerian derivation of the fractional advection-dispersion equation” by Schumer, Benson, Meerschaert, and Wheatcraft.
[38] Fangying Song, Title: “Fractional Spectral Vanishing Viscosity method for Surface Quasi-Geostrophic equation”.
[37] Xiaoning Zheng, Title: “Fractional Laplacian in complex-Geometry 2D and 3D domains”.
[36] Zhiping Mao, Title: “SVV-LDG method for the fractional Burgers equation with nonlinear non-locality”.
[35] Fanhai Zeng, Title: “IMEX methods for nonlinear fractional ordinary differential equations”.
[34] Anna Lischke, Title: “The numerical solution of linear multi-term fractional differential equations: systems of equations” by Edwards, Ford, and Simpson.
[33] Jorge Suzuki, Title: “A fractional-order uniaxial visco-elasto-plastic model with damage for structural analysis.”
[32] Xuejuan Chen, Title: “A novel high order space-time spectral method for the time fractional fokker-planck equation” by Minling Zhen, Fawang Liu, Ian Turner, and Vo Anh.
[31] Mamikon Gulian, Title: “Fast convolution for non reflecting boundary conditions,” by Christian Lubich and Achim Schadle.
[30] Fangying Song, Title: “A speculative study of 2/3-order fractional Laplacian modeling of turbulence: Some thoughts and conjectures”, by Wen Chen (2006).
[29] Zhiping Mao, Title: “Non-uniqueness of weak solutions for fractal Burgers equation ” by N. Alibaud and B. Andreianov.
[28] Mamikon Gulian, Title: “A memory principle for time fractional differential equations”
[27] Fanhai Zeng, Title: “Finite difference methods for multi-term fractional ordinary differential equations”.
[26] Jorge Suzuki, Title: “Lemaitre's damage applied to a fractional-order visco-elasto-plastic model”.
[25] Zhiping Mao, Title: “Fourier Spectral Method for Fractional Allen-Cahn Equation”.
[24] Anna Lischke, Title: “Tunably accurate Laguerre Petrov-Galerkin spectral methods for FODEs”.
[23] Markus Sarkis, Title: “A Parareal method for time-fractional differential equations”, a paper by Qinwu Xu, Jan Hesthaven, and Feng Chen.
[22] Xuejuan Chen, Title: “Some high-order difference schemes for the distributed-order differential equations”
[21] Zhiping Mao, Title: “Local Discontinuous Galerkin Method for Fractional Burgers Equations with Nonlocal Nonlinearity”
[20] Xuan Zhao, Title: “An introductory example of fractional differential equation using Hierarchical matrices”
[19] Fanhai Zeng, Title: “A generalized spectral collocation method with tunable accuracy for variable-order fractional differential equations”
[18] Anna Lischke, Title: “Fractional integration by parts in Petrov-Galerkin spectral methods with tunable accuracy”
[17] Fangying Song, Title: “A fractional Allen-Cahn equation”
[16] Jorge Suzuki, Title: “Estimation of shear modulus in media with power law characteristics”, paper by W. Zhang and S. Holm, to be published in the Journal of Ultrasonics 64 (2016).
[15] Fanhai Zeng, Title: “Spectral collocation method for fractional boundary value problems”
[14] Anna Lischke, Title: “Measuring memory with the order of fractional derivative”, paper by Maolin Du, Zihua Wang, and Haiyan Hu
[13] Dongkun Zhang, Title: “Coupled simulations of stochastic multi-scale systems”
[12] Fanhai Zeng, Title: “Numerical methods for variable-order fractional differential equations”
[11] Fangying Song, Title: “Definitions of variable-order fractional derivatives”
[10] Fanhai Zeng, Title: “Fractional-order Legendre functions”
[9] Anna Lischke, Title: “Variable-order fractional numerical differentiation using wavelets”
[8] Dongkun Zhang, Title: “Stochastic Collocation Algorithms Using L1-Minimization for Bayesian Solution of Inverse Problems” paper by Liang Yan and Lin Guo.
[7] Xuejuan Chen, Title: “Introduction of My Research”
[6] Zhiping Mao, Title: “Efficient and High Order Spectral Methods for Fractional Differential Equations”
[5] Fanhai Zeng, Title: “Stable multi-domain spectral penalty methods for fractional partial differential equations” by Qinwu Xu and Jan S. Hesthaven
[4] Fangying Song, Title: “Rigorous treatment of boundary condition via spectral technique for space-fractional equations on finite insulated one-dimensional domains”, paper by N. Cusimano et al.
[3] Wei Cai, Title: “Modeling power law absorption and dispersion in viscoelastic solids using a split-field and the fractional Laplacian”, paper by Bradley E. Treebyb and B. T. Cox, JASA, 2014
[2] Fangying's presentation, Title: “A Discretization Scheme for Time Fractional Wave Equation”
[1] Mengdi Zheng, Title: “Fractional Dynamics on networks:Anomalous Diffusion and Levy Flights”, paper by A.P. Riascos and Jose L. Mateos, 2014
Publications
[1] Paris Perdikaris, G. E. Karniadakis (2014), “ Fractional-order viscoelasticity in one-dimensional blood flow models ”, Annals of biomedical engineering, 42 (5), 1012-1023, Springer.
[2] M. Zayernouri, G. E. Karniadakis (2013) “Fractional Sturm-Liouville Eigen-Problems: Theory and Numerical Approximations”, Journal of Computational Physics, 47-3, 2108–2131.
[3] M. Zayernouri, G. E. Karniadakis (2014) “Exponentially Accurate Spectral and Spectral Element Methods for Fractional ODEs”, Journal of Computational Physics, 257, 460–480.
[4] M. Zayernouri, W. Cao, Z. Zhang, G. E. Karniadakis (2014) “Spectral and Discontinuous Spectral Element Methods for Fractional Delay Equations”, SIAM Journal on Scientific Computing, Vol. 36 (6), B904–B929.
[5] M. Zayernouri, G. E. Karniadakis (2014) “Discontinuous Spectral Element Methods for Time- and Space-Fractional Advection Equations”, SIAM Journal on Scientific Computing, 36 (4), B684–B707.
[6] M. Zayernouri, G. E. Karniadakis (2014) “Fractional Spectral Collocation Method”, SIAM Journal on Scientific Computing, 36 (1), A40–A62.
[7] M. Zayernouri, G. E. Karniadakis (2014) “Fractional Spectral Collocation Methods for Linear and Nonlinear Variable Order Fractional PDEs”, Journal Computational Physics, Special Issue on Fractional PDEs, Accepted.
[8] M. Zayernouri, M. Ainsworth, and G. E. Karniadakis (2014) “A Unified Petrov-Galerkin Spectral Method for Fractional PDEs”, Computer Methods in Applied Mechanics and Engineering (CMAME), Accepted.
[9] M. Zayernouri, M. Ainsworth, and G. E. Karniadakis (2014) “Tempered Fractional Sturm-Liouville Eigen-Problems”, SIAM Journal on Scientific Computing, Submitted.
[10] M. Zheng and G.E. Karnidakis, Numerical Methods for SPDEs with tempered stable processes, Submitted to SIAM J. Sci. Comput. 2014.
[11] Xuan Zhao, Zhi-zhong Sun, George Em Karniadakis, Second order approximations for variable order fractional derivatives: Algorithms and applications, Journal of Computational Physics, Special Issue on Fractional PDEs, (2014) doi:10.1016/j.jcp.2014. 08.015
[12] F. Song, C. Xu, G.E. Karniadakis, A fractional phase-field model for two-phase flows with tunable sharpness: Algorithms and simulations, Computer Methods in Applied Mechanics and Engineering, 305 (2016), 376-404.
[13] J.L. Suzuki, M. Zayernouri, M.L. Bittencourt, G.E. Karniadakis, Fractional-order uniaxial visco-elasto-plastic models for structural analysis, Computer Methods in Applied Mechanics and Engineering, 308 (2016), 443-467.